Class 8 Maths Ganita Prakash Chapter 1 A Square and A Cube NCERT Solutions
Class 8 Maths Ganita Prakash Chapter 1 A Square and A Cube NCERT Solutions guides students in solving the problems related to the first chapter of Class 8 Maths.
Textbook Page 1 – 3
Q. Before the process begins, Khoisnam realises that he already knows which lockers will be open at the end. How did he figure out the answer?
Hint: Find out how many times each locker is toggled.
Solution:
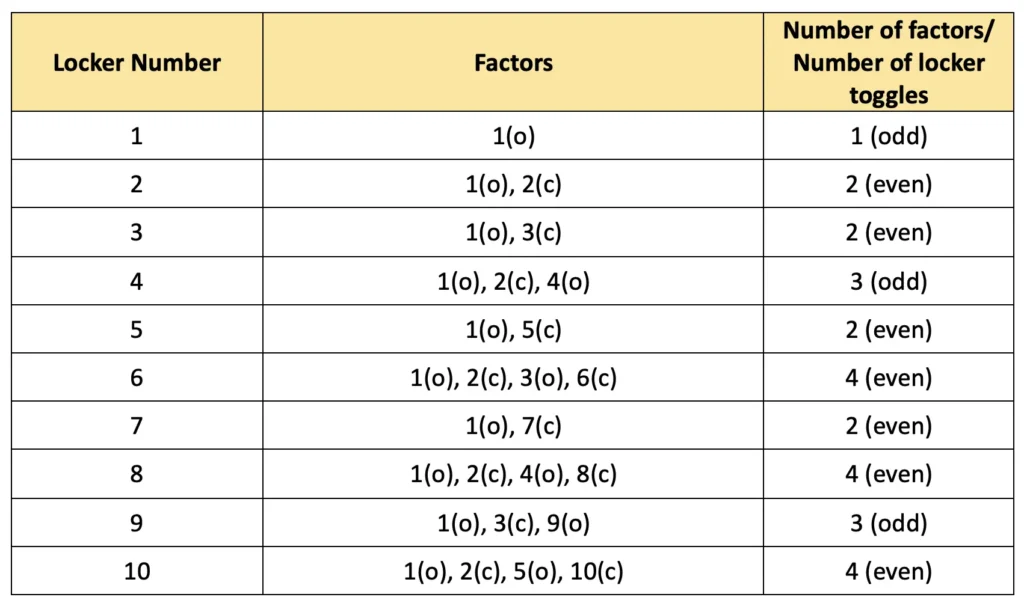
He noticed that the number of toggles a locker receives equals the number of factors of that locker’s number. A locker toggled an odd number of times will be open at the end; a locker toggled an even number of times will be closed. Only perfect squares have an odd number of factors, so exactly the lockers numbered with perfect squares (1, 4, 9, 16, …) remain open.
Q. Does every number have an even number of factors?
Solution:
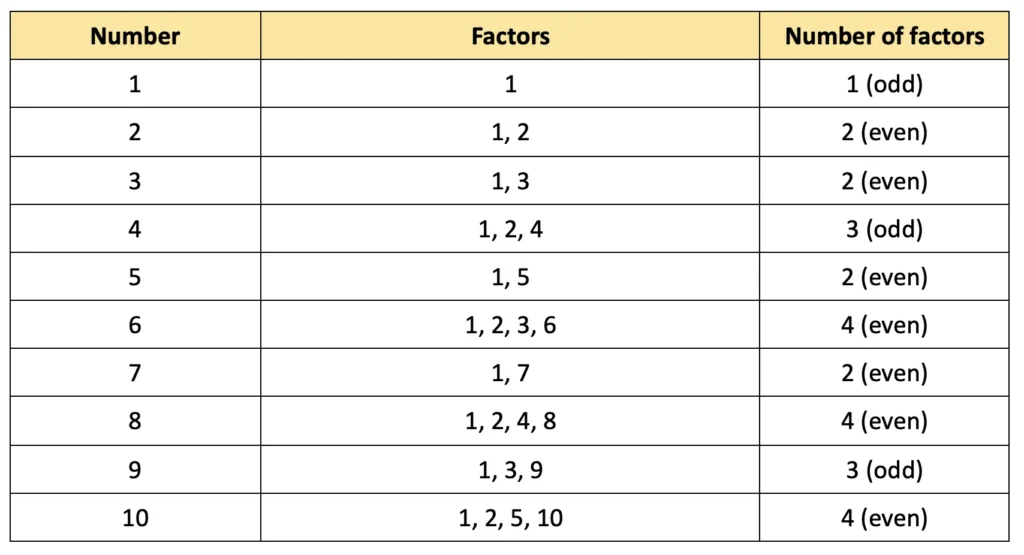
Not every number has an even number of factors. Only perfect squares have an odd number of factors, because they each have one factor which, when multiplied by itself, equals the number.
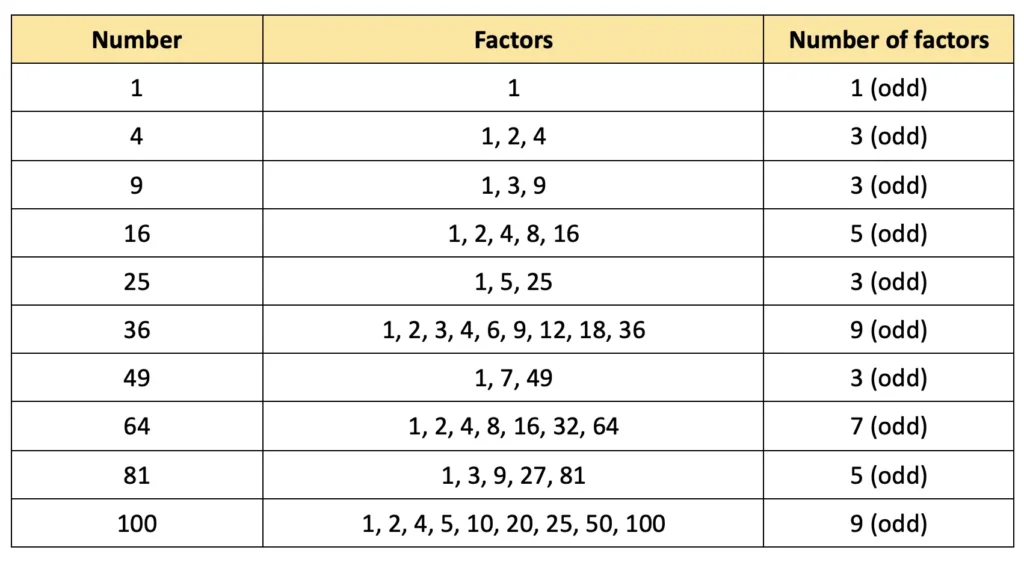
Q. Can you use this insight to find more numbers with an odd number of factors?
Solution:
Q. Write the locker numbers that remain open.
Solution:
10 lockers with square locker numbers, i.e, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, will remain open.
Q. Which are these five lockers?
Solution:
The lockers that are toggled twice are the prime numbers, since each prime number has 1 and the number itself as factors. So, the code is 2-3-5-7-11.
Textbook Page 4
Q. Find the squares of the first 30 natural numbers and fill in the table below.
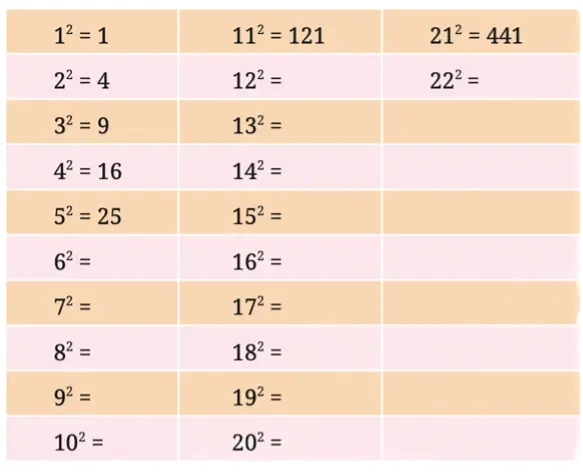
Solution:
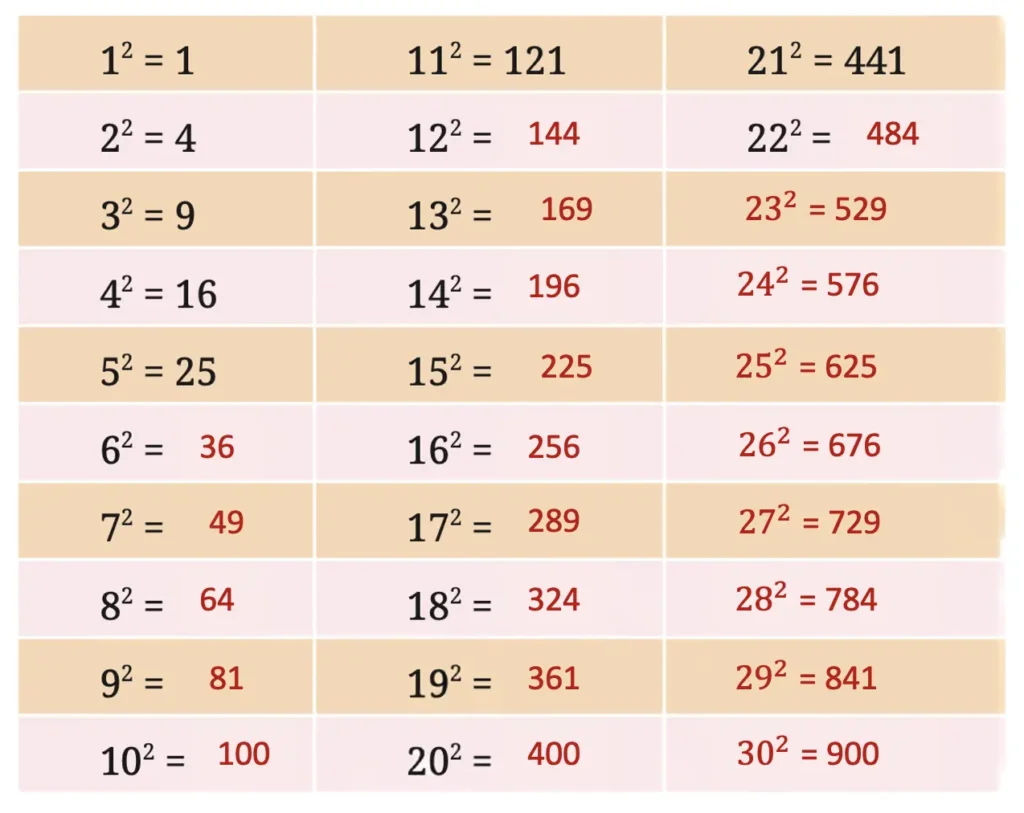
Q. What patterns do you notice? Share your observations and make conjectures.
Solution:
All perfect square numbers end with 0, 1, 4, 5, 6, or 9, and none of them end with 2, 3, 7, or 8.
Q. If a number ends in 0, 1, 4, 5, 6, or 9, is it always a square?
Solution:
We cannot determine if a number is a square just by looking at the digit in the units place. But the unit digit can tell us when a number is not a square. If a number ends with 2, 3, 7, or 8, then we can say that it is not a square. For example, 26 ends in 6 but is not a perfect square.
Q. Write 5 numbers such that you can determine by looking at their unit digit that they are not squares.
Solution:
478, 1072, 7543, 9047, and 1257.
Textbook Page 5
Q. Which of the following numbers have the digit 6 in the units place?
(i) 382 (ii) 342 (iii) 462 (iv) 562 (v) 742 (vi) 822
Solution:
(i) 382
38 → Units digit → 8
8 × 8 = 64 (ends in 4)
So, 382 does not end in 6.
(ii) 342
34 → Units digit → 4
4 × 4 = 16 (ends in 6)
So, 342 ends in 6.
(iii) 462
46 → Units digit → 6
6 × 6 = 36 (ends in 6)
So, 462 ends in 6.
(iv) 562
56 → Units digit → 6
6 × 6 = 36 (ends in 6)
So, 562 ends in 6.
(v) 742
74 → Units digit → 4
4 × 4 = 16 (ends in 6)
So, 742 ends in 6.
(vi) 822
82 → Units digit → 2
2 × 2 = 4 (ends in 4)
So, 822 ends in 4.
Thus, a number with the last digit 4 or 6 has 6 as the last digit in its square.
Therefore, 342 , 462 ,562 ,742 are the numbers that have the digit 6 in the units place.
Q. Consider the following numbers and their squares.
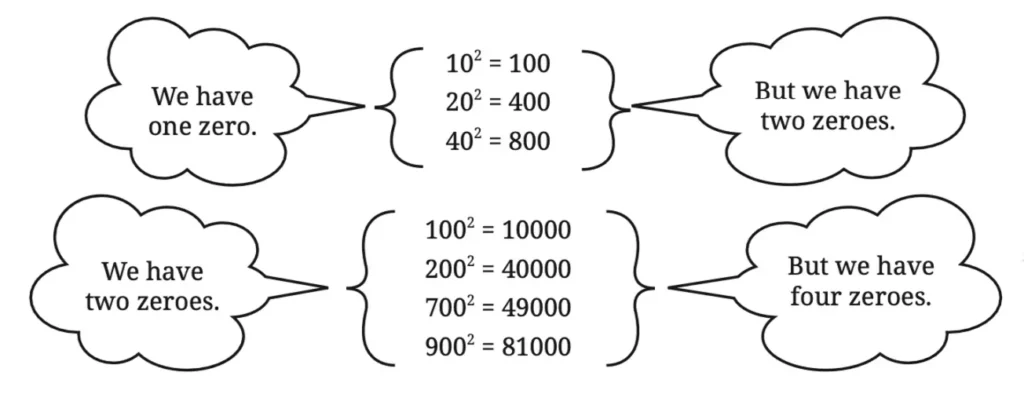
If a number contains 3 zeros at the end, how many zeros will its square have at the end?
Solution:
The number of zeros at the end of the square of a number is always double the number of zeros at the end of the original number. Therefore, if a number contains 3 zeros at the end, then its square will have 6 zeros.
Q. What do you notice about the number of zeros at the end of a number and the number of zeros at the end of its square? Will this always happen? Can we say that squares can only have an even number of zeros at the end?
Solution:
The number of zeros at the end of the square of a number is always double the number of zeros at the end of the original number. Yes, this will always happen. Yes, we can say that the square can only have an even number of zeros at the end.
Q. What can you say about the parity of a number and its square?
Solution:
The square of an even number is always even, and that of an odd number is always odd.
Textbook Page 7
Q. Find how many numbers lie between two consecutive perfect squares. Do you notice a pattern?
Solution:
There are exactly ‘2n’ numbers between n2 and (n + 1)2. For example: Between 32(n) and 42(n + 1) there are 2 × 3 = 6 (2n) numbers.
Q. How many square numbers are there between 1 and 100? How many are between 101 and 200? Using the table of squares you filled earlier, enter the values below, tabulating the number of squares in each block of 100. What is the largest square less than 1000?
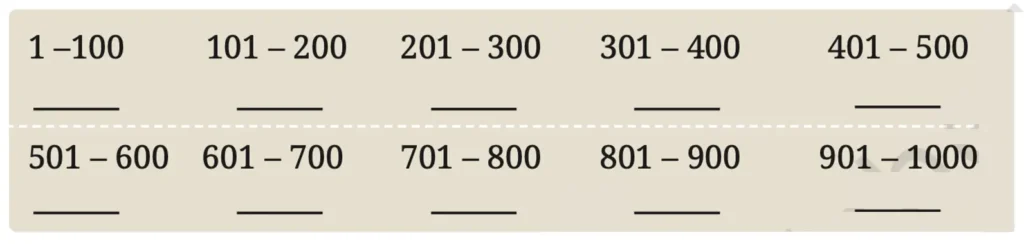
Solution:
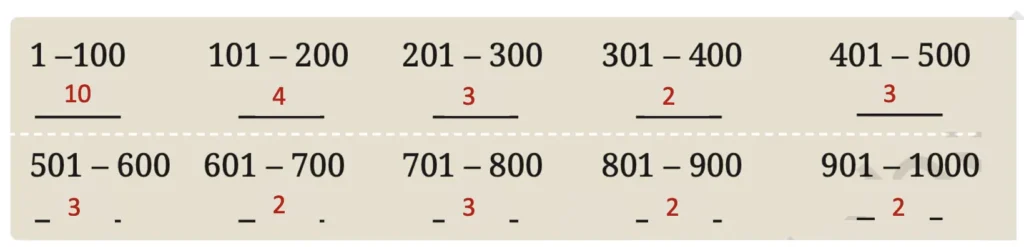
The largest square less than 1000 is 312 = 961.
Q. Can you see any relation between triangular numbers and square numbers? Extend the pattern shown and draw the next term.
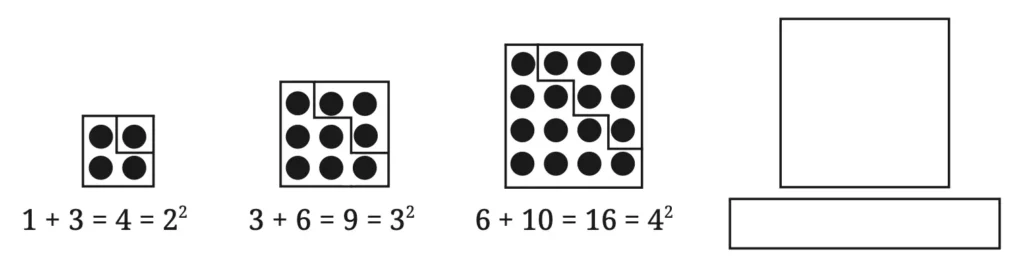
Solution:
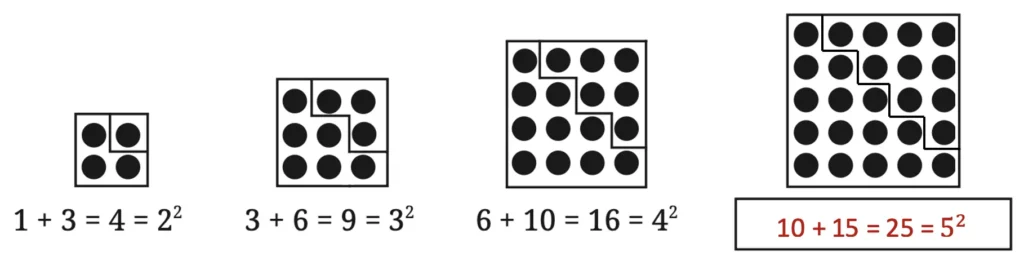
Textbook Page 9
Q. Find whether 1156 and 2800 are perfect squares using prime factorisation.
Solution:
(i) 1156 = (2 × 2) × (17 × 17)
= 22 × 172
= (2 × 17)2
= (34)2
∴ √1156 = 34.
(ii) 2800 = (2 × 2) × (2 × 2) × (5 × 5) × 7
= 22 × 22 × 52 × 7
Since the factors cannot be paired
∴ 2800 is not a perfect square.
Textbook Page 10 – 11
Figure it Out
1. Which of the following numbers are not perfect squares?
(i) 2032
(ii) 2048
(iii) 1027
(iv) 1089
Solution:
A perfect square ends in 0, 1, 4, 5, 6, or 9 at its unit’s place.
(i) 2032 ends in 2 at the unit’s place. So, it is not a perfect square.
(ii) 2048 ends in 8 at the unit’s place. So, it is not a perfect square.
(iii) 1027 ends in 7 at the unit’s place. So, it is not a perfect square.
(iv) 1089 ends in 9 at the unit’s place. So, it is a perfect square.
2. Which one among 642, 1082, 2922, 362 has the last digit 4?
Solution:
(i) 642
The unit’s digit of 64 is 4
4 × 4 = 16 (last digit 6)
(ii) 1082
The unit’s digit of 108 is 8
8 × 8 = 64 (last digit 4)
(iii) 2922
The unit’s digit of 292 is 2
2 × 2 = 4 (last digit 4)
(iv) 362
The unit’s digit of 36 is 6
6 × 6 = 36 (last digit 6)
Therefore, 1082 and 2922 have 4 as their last digits.
3. Given 1252 = 15625, what is the value of 1262?
(i) 15625 + 126
(ii) 15625 + 262
(iii) 15625 + 253
(iv) 15625 + 251
(v) 15625 + 252
Solution:
1252 = 15625
This means 15625 is the sum of the first 125 odd numbers.
1262 = 15625 + 127th odd number
127th odd number = (2 × 127) – 1 = 252 – 1 = 251.
∴ 1262 = 15625 + 251
Therefore, (iv) 15625 + 251 is the correct answer.
4. Find the length of the side of a square whose area is 441 m2.
Solution:
Area of the square = side × side = 441 m2.
(side)2 = 441
side = √441
side = ± 21 m
Since the side of a square cannot be negative, the length of the side of the square is 21 m.
5. Find the smallest square number that is divisible by each of the following numbers: 4, 9, and 10.
Solution:
The L.C.M. of 4, 9, and 10 is 180.
So, the smallest number divisible by 4, 9, and 10 is 180.
180 = 2 × 2 × 3 × 3 × 5
180 = 22 × 32 × 5
Here, 5 has no pair.
So, 180 is not a perfect square. To make it a perfect square, we multiply it by 5.
Hence, the required smallest square number is 180 × 5 = 900.
6. Find the smallest number by which 9408 must be multiplied so that the product is a perfect square. Find the square root of the product.
Solution:
9408 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 7 × 7
9408 = 22 × 22 × 22 × 72 × 3
Here, 3 has no pair.
So, 9408 is not a perfect square. To make it a perfect square, we multiply it by 3.
Therefore, 9408 × 3 = 28224, which is a perfect square.
√28224 = √2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
√28224 = √22 × 22 × 22 × 32 × 72
∴ √28224 = 2 × 2 × 2 × 3 × 7 = 8 × 21 = 168.
7. How many numbers lie between the squares of the following numbers?
(i) 16 and 17 (ii) 99 and 100
Solution:
There are 2n numbers between n2 and (n + 1)2 .
(i) 162 and 172
Here, n = 16 and (n + 1) = 17
Therefore, the numbers between 162 and 172 = 2n = 2 × 16 = 32.
(ii) 992 and 1002
Here, n = 99 and (n + 1) = 100
Therefore, the numbers between the squares 992 and 1002 = 2n = 2 × 99 = 198.
8. In the following pattern, fill in the missing numbers:
12 × 22 × 22 = 32
22 × 32 × 62 = 72
32 × 42 × 122 = 132
42 × 52 × 202 = (___)2
92 × 102 × (___)2 = (___)2
Solution:
12 × 22 × 22 = 32
22 × 32 × 62 = 72
32 × 42 × 122 = 132
42 × 52 × 202 = (21)2
92 × 102 × (90)2 = (91)2
9. How many tiny squares are there in the following picture? Write the prime factorisation of the number of tiny squares.

Solution:
Number of squares in a row = 9.
Number of squares in a column = 9.
Total number of squares in the picture = 9 × 9 = 81.
Number of tiny squares in a square = 5 × 5 = 25.
Total number of tiny squares in the picture = 25 × 81 = 2025.
Prime factorization of 2025:
2025 = (3 × 3) × (3 × 3) × (5 × 5)
2025 = 32 × 32 × 52
2025 = 34 × 52.
Textbook Page 12
Q. Complete the table below.
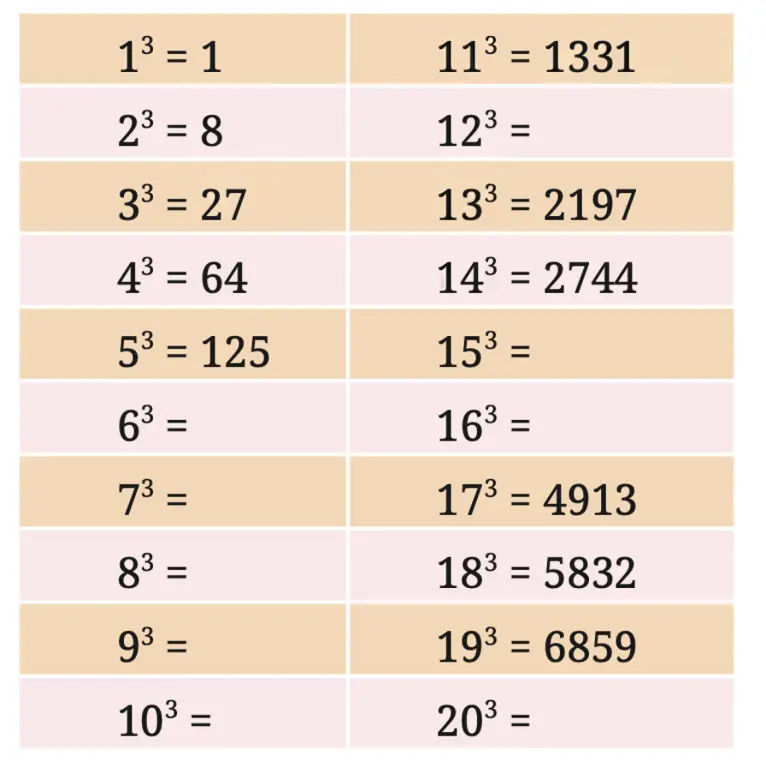
Solution:
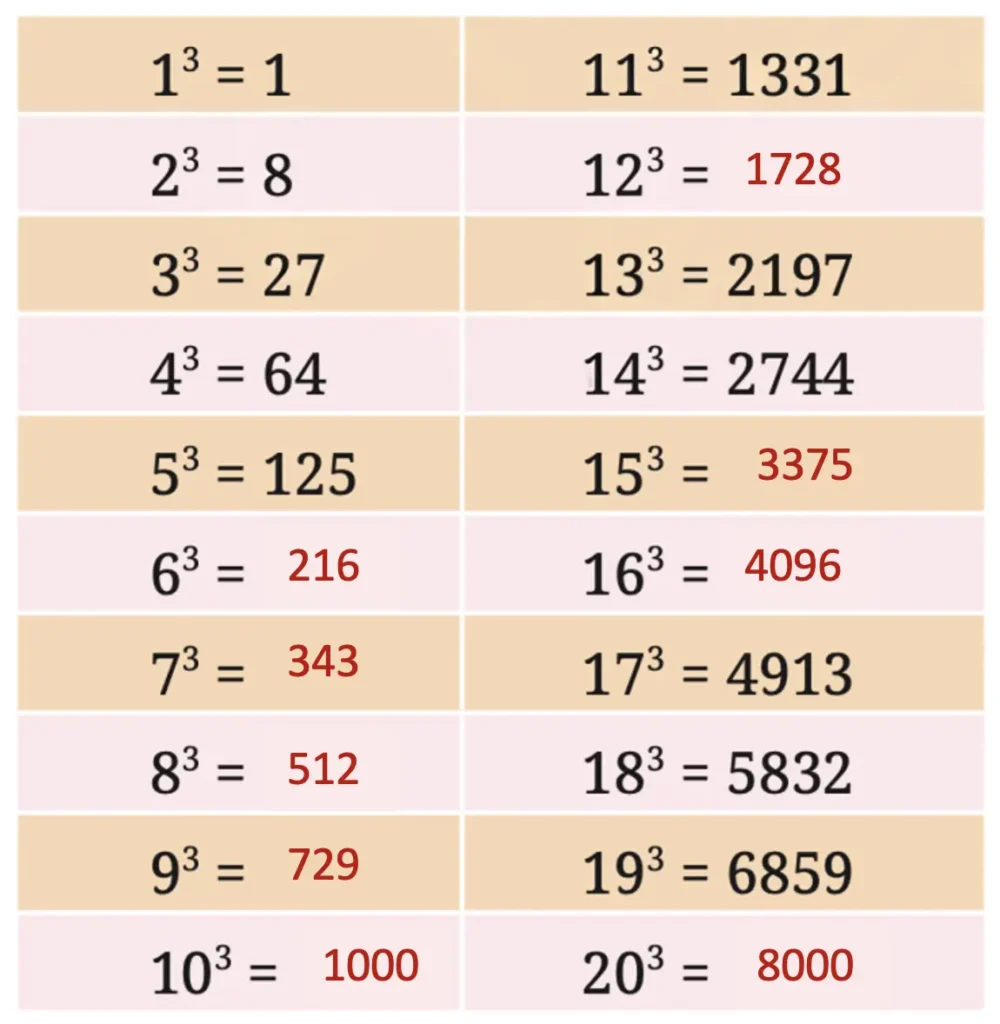
Q. What patterns do you notice in the table above?
Solution:
(i) Cube of a number with the last digit 1 ends in 1.
(ii) The cube of a number ending in 2 has the last digit 8, and the cube of a number ending in 8 has the last digit 2.
(iii) The cube of a number ending in 3 has the last digit 7, and the cube of a number ending in 7 has the last digit 3.
(iv) When cubed, numbers ending in 4, 5, 6, 9, or 0 keep the same unit’s digit
Q. We know that 0, 1, 4, 5, 6, 9 are the only last digits possible for squares. What are the possible last digits of cubes?
Solution:
The last digits of cubes can be any digit from 0 to 9.
Textbook Page 13
Q. Similar to squares, can you find the number of cubes with 1 digit, 2 digits, and 3 digits? What do you observe?
Solution:
1-digit cubes: 13 = 8, 23 = 8
Count: 2 cubes (1, 8)
2-digit cubes: 33 = 27, 43 = 64
Count: 2 cubes (27, 64)
3-digit cubes: 53 = 125, 63 = 216, 73 = 343, 83 = 512, 93 = 729
Count: 5 cubes (125, 216, 343, 512, 729)
The number of perfect cubes increases as the numbers get larger.
Unlike squares, cubes grow more quickly, so fewer cubes fit into smaller ranges.
Q. Can a cube end with exactly two zeroes (00)? Explain.
Solution:
No. A cube cannot end with exactly two zeros because zeros in a cube occur in multiples of three. If a number ends in one zero, its cube ends in three zeros.
Q. The next two taxicab numbers after 1729 are 4104 and 13832. Find the two ways in which each of these can be expressed as the sum of two positive cubes.
Solution:
4104:
23 + 163 = 8 + 4096 = 4104
93 + 153 = 729 + 3375 = 4104
13832:
23 + 243 = 8 + 13824 = 13832
183 + 203 = 5832 + 8000 = 13832
Textbook Page 14
Q. Can you tell what this sum is without doing the calculation?
91 + 93 + 95 + 97 + 99 + 101 + 103 + 105 + 107 + 109.
Solution:
This series has 10 consecutive odd numbers, and their sum is 103 = 1000.
Textbook Page 15
Q. Find the cube roots of these numbers:
(i) ∛64 = (ii) ∛512 = (iii) ∛729 =
Solution:
(i) ∛64
64 = (2 × 2 × 2) × (2 × 2 × 2)
= 23 × 23
= (2 × 2)3 = 43
∴ ∛64 = 4.
(ii) ∛512
512 = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2)
= 23 × 23 × 23
= (2 × 2 × 2)3 = 83
∴ ∛512 = 8.
(iii) ∛729
729 = (3 × 3 × 3) × (3 × 3 × 3)
= 33 × 33
= (3 × 3)3 = 93
∴ ∛729 = 9.
Textbook Page 16 – 17
Figure it Out
1. Find the cube roots of 27000 and 10648.
Solution:
(i) ∛27000
Prime factorization of 27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5
27000 = 23 × 33 × 53
27000 = (2 × 3 × 5)3
27000 = 303
∴ ∛27000 = 30.
(ii) ∛10648
Prime factorisation of 10648 = 2 × 2 × 2 × 11 × 11 × 11
10648 = 23 × 113
10648 = (2 × 11)3
10648 = 223
∴ ∛10648 = 22.
2. What number will you multiply by 1323 to make it a cube number?
Solution:
Prime factorization of 1323 = 3 × 3 × 3 × 7 × 7
Here, there is no triplet of 7.
So, 1323 is not a perfect cube. To make it a cube number, we multiply it by 7.
1323 × 7 = 3 × 3 × 3 × 7 × 7 × 7 = 9261 which is a perfect square.
Hence, the number by which 1323 needs to be multiplied to make it a cube number is 7.
3. State true or false. Explain your reasoning.
(i) The cube of any odd number is even.
(ii) There is no perfect cube that ends with 8.
(iii) The cube of a 2-digit number may be a 3-digit number.
(iv) The cube of a 2-digit number may have seven or more digits.
(v) Cube numbers have an odd number of factors.
Solution:
(i) False because the cube of an odd number is always odd.
For example: 33 = 27, 53 = 125, 73 = 343, all are odd.
(ii) False because some cubes do end with 8.
For example: 23 = 8, 123 = 1728, both end with 8.
(iii) False, because the cube of a 2-digit number can range from 4-digit to 6-digit numbers.
For example: 103 = 1000, 993 = 970299.
(iv) False because the largest 2-digit number ’99’ has a cube that is a 6-digit number, i.e. 993 = 970299.
So, a 2-digit whole number will always have a cube with at most 6 digits.
(v) False because only perfect squares have an odd number of factors.
For example:
Factors of 8 = 1, 2, 4, 8 → 4 factors (even).
Factors of 27 = 1, 3, 9, 27 → 4 factors (even).
4. You are told that 1331 is a perfect cube. Can you guess without factorisation what its cube root is? Similarly, guess the cube roots of 4913, 12167, and 32768.
Solution:
(i) Yes, the cube root of 1331 can be guessed without factorization.
103 = 1000 and 203 = 8000
So, 10 < ∛1331 < 20
Since 1331 ends in 1, its cube root ends in 1.
The number between 10 and 20 that ends in 1 is 11.
∴ ∛1331 = 11.
(ii) ∛4913
103 = 1000 and 203 = 8000
So, 10 < ∛4913 < 20
Since 4913 ends in 3, its cube root ends in 7.
The number between 10 and 20 that ends in 7 is 17.
∴ ∛4913 = 17.
(iii) ∛12167
203 = 8000 and 303 = 27000
So, 20 < ∛12167 < 30
Since 12167 ends in 7, its cube root ends in 3.
The number between 20 and 30 that ends in 3 is 23.
∴ ∛12167 = 23.
(iv) ∛32768
303 = 27000 and 403 = 64000
So, 30 < ∛32768 < 40
Since 32768 ends in 8, its cube root ends in 2.
The number between 30 and 40 that ends in 2 is 32.
∛32768 = 32.
5. Which of the following is the greatest? Explain your reasoning.
(a) 673 – 663
(b) 433 – 423
(c) 672 – 662
(d) 432 – 422
Solution:
Using, n3 − (n−1)3 = 3n2 − 3n + 1;
n2 − (n−1)2 = 2n−1.
(a) 673 – 663 = 3 × 672 – 3 × 67 + 1
= 3 × 4489 – 201 + 1
= 13467 – 200 = 13267.
(b) 433 – 423 = 3 × 432 – 3 × 43 + 1
= 3 × 1848 – 129 + 1
= 5547 – 128 = 5419.
(c) 672 – 662 = 2 × 67 – 1
= 134 – 1 = 133.
(d) 432 – 422 = 2 × 43 – 1
= 86 – 1 = 85.
Thus, (i) 673 – 663 is the greatest.
