Class 4 Maths Mela Chapter 3 Patterns Around Us NCERT Solutions
Class 4 Maths Mela Chapter 3 Patterns Around Us NCERT Solutions have been updated for the academic year 2025–26. These solutions provide all the necessary help to solve problems from Chapter 3, Patterns Around Us. They are intended to facilitate learning and guide Class 4 students. The solutions are written in simple language and easy-to-understand sentences suitable for young learners. The chapter includes topics such as counting, multiplication, addition, money-related problems, and understanding the difference between even and odd numbers.
Class 4 Maths Mela Chapter 3 Patterns Around Us Questions Answers – PDF Download
Page 34
Let Us Count

Q. Gundappa has some land with tall coconut trees. How many coconut trees does Gundappa have?
Solution:
Total trees = 9 × 9 = 81.
Q. How do you know?
Solution:
It is calculated by counting the number of trees in a group and then multiplying it by 9 to get the total number of trees.
Q. Gundappa has plucked 5 coconuts from each tree. How many coconuts has he plucked?
Solution:
Total trees = 81
Coconuts plucked from each tree = 5
Total coconuts plucked = 81 × 5 = 405 coconuts.

Q. Muniamma makes plates and cups. Number of cups = ________
Solution:
Total cups = 2 × 11 + 2 × 10 + 2 × 9
= 22 + 20 + 18 = 60 cups.
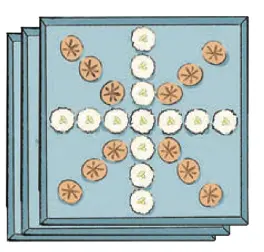
Q. How many coconut laddoos are there in the trays? ____________
Solution:
Total laddoos = 3 × 4 = 12 laddoos.
Q. How many milk pedas are there in the trays? ____________
Solution:
Total pedas = 3 × 4 + 1 = 12 + 1 = 13 pedas.
Page 35
Patterns with Money

Q. How much money?
Solution:
Total money = 4 × ₹5 + 4 × ₹10 + ₹20 = ₹20 + ₹40 + ₹20 = ₹80.

Q. How much money? ________
Solution:
Total money = 8 × ₹5 + 6 × ₹10 + 4 × ₹2 = ₹40 + ₹60 + ₹8 = ₹108.
Q. How did you count them? Discuss in class.
Solution:
It is done by multiplying the number of notes of each denomination by the value of the note, then adding the amounts together.
Q. Arrange play money of amounts 1, 2, 5, and 10 to show ₹36, ₹125, and ₹183. Ask your peers to tell how much it is.
Solution:
Solution:
₹36 = 4 × ₹10 + ₹5 + ₹1.
₹125 = 10 × ₹10 + 5 × ₹5.
₹183 = 15 × ₹10 + 6 × ₹5 + 3 × ₹1.
Two Ways
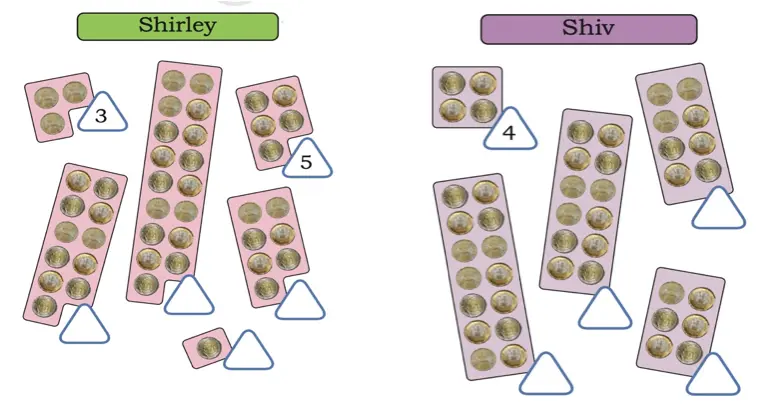
Q. Shirley and Shiv arranged their coins in the following ways. Write the number of coins in the triangles.
Solution:
Page 36
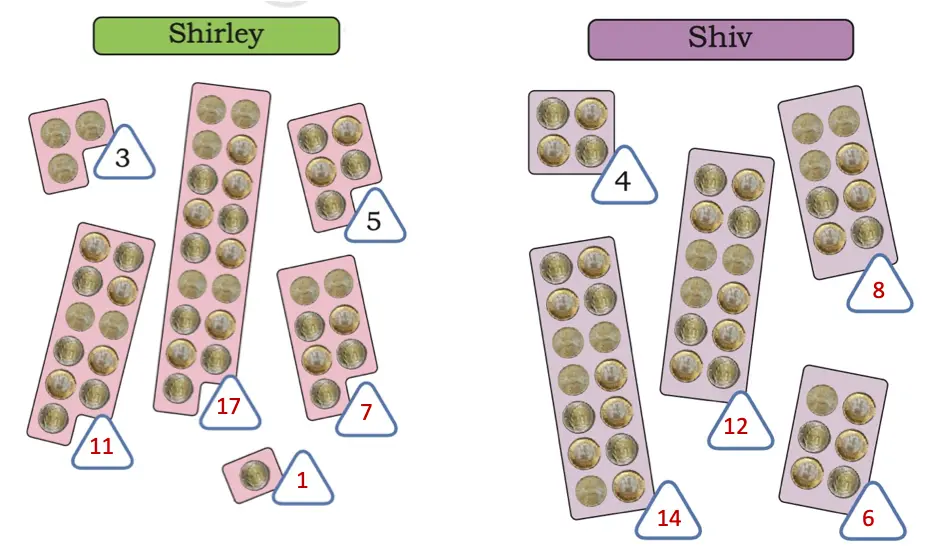
Q. Describe Shiv’s arrangement and write his numbers.
Solution:
Shiv arranged coins in groups of even numbers, and his numbers are 4, 6, 8, 12, and 14.
Q. Describe Shirley’s arrangement and write her numbers.
Solution:
Shirley arranged coins in groups of odd numbers, and her numbers are 1, 3, 5, 7, 11, and 17.
Q. Identify numbers between 1 and 20 as even or odd. You may draw the pairing arrangement of the numbers.
Solution:

Page 37
Crayons Arrangement
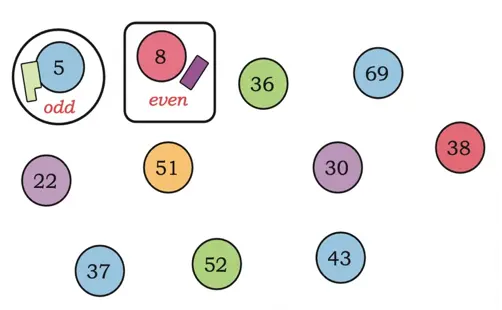
Q. Circle the odd numbers and put a square around each even number. Use the crayons arrangement, if needed.
Solution:
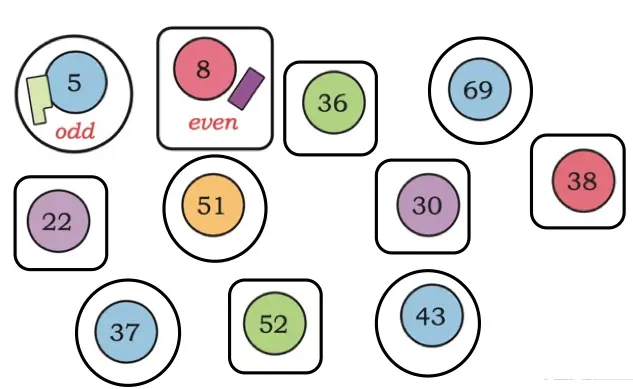
Q. Which numbers are even and which are odd? Discuss.
Solution:
Numbers divisible by 2 are called even numbers (e.g., 42, 30, 28), and numbers not divisible by 2 are called odd numbers (e.g., 17, 91, 47).
Q. Shirley observes an interesting even-odd pattern in the page numbers of her Maths book. Explore your textbook and find out what Shirley has seen. Draw a square on the even numbers. Put a circle on the odd numbers.
Solution:
An interesting pattern is that odd-numbered pages are on the right side, while even-numbered pages are on the left.
Page 38
Q. Identify which of the following numbers are even and which are odd. Explain your reasoning.

Solution:
Odd numbers: 67, 415, 99.
Even numbers: 30, 46, 78, 300, 154.
Q. Make two 2-digit numbers using the digits 1 and 6 without repetition. Identify the numbers as even or odd.
Solution:
16 and 61. 16 is even, and 61 is odd.
Q. Now choose any two digits and make 2-digit numbers in such a way that the numbers are even.
Solution:
Digits: 4 and 7
Numbers: 47 and 74. 47 is odd and 74 is even.
Q. Are there more even or odd numbers between 1 and 100?
Solution:
There are 50 odd and 50 even numbers between 1 and 100.
Q. Shirley notices that both the numbers, before and after an odd number, are even. Shiv wonders if both the numbers, before and after an even number, will be odd. What do you think? Check and discuss.
Solution:
Yes, Shiv is right. An even number always lie between two odd numbers when counted in order. For example, in 3, 4, 5 — 4 is even, and both 3 and 5 are odd.
Q. Choose any 10 numbers in order without skipping any (consecutive numbers). Write whether they are even or odd below each number. What do you notice? Discuss.
Solution:

Even and odd numbers appear in alternate patterns.
