Class 5 Maths Mela Chapter 3 Angles as Turns NCERT Solutions

Textbook Page 32

Q. Can you recognise the child in the picture who has made a full turn? Who has made a half turn? How do you know? Discuss in class.

Solution:
Child C has made a full turn because, in the second image, C is facing the same direction as in the first image, which means they turned all the way around, i.e., 360°.
Child A has made a half turn because, in the second image, A is facing the opposite direction compared to the first image, meaning they have turned halfway around, i.e., 180°.

Q. Give examples of real-life situations where you observe turns.
Solution:
1. Riding a merry-go-round.
2. Opening a bottle cap.
3. Turning a doorknob to open a door.
4. Turning the handle of a bicycle or the steering wheel of a car.
5. Dancer making quarter, half, or full turns.
6. Turning a key in a lock.

Textbook Page 33

A giant wheel makes a full turn when it comes back to the starting position E.

Reema takes two half turns in the same direction. It is like a complete turn.
What happens if she takes 2 quarter turns in the same direction?
It is like a half turn.
What happens if she takes 4 quarter turns in the same direction?
It is like a complete turn.

Q. Write some of the everyday objects that involve turns. For example, taps, __________, __________, __________, __________, and __________.
Solution:
Taps, door knobs, steering wheels, bottle caps, keys, and merry-go-rounds.

Q. What is the maximum possible turn in each of these cases? Check and tick.

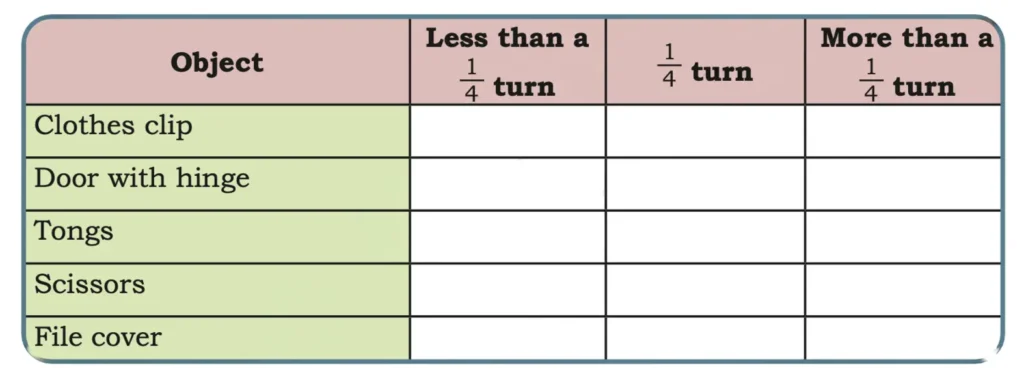
Solution:

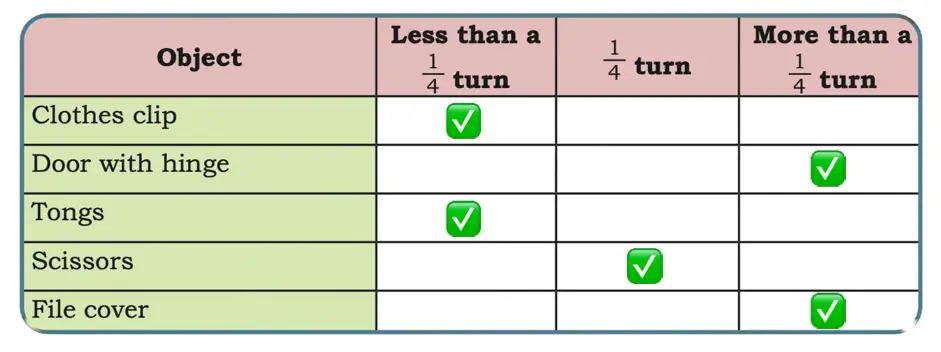
Q. Do any of the above objects make a half turn? Write their names below—
Solution:
None.

Q. Do any of the above objects make a full turn? Write their names below—
Solution:
File cover.

Textbook Page 34 – 36

Let Us Do

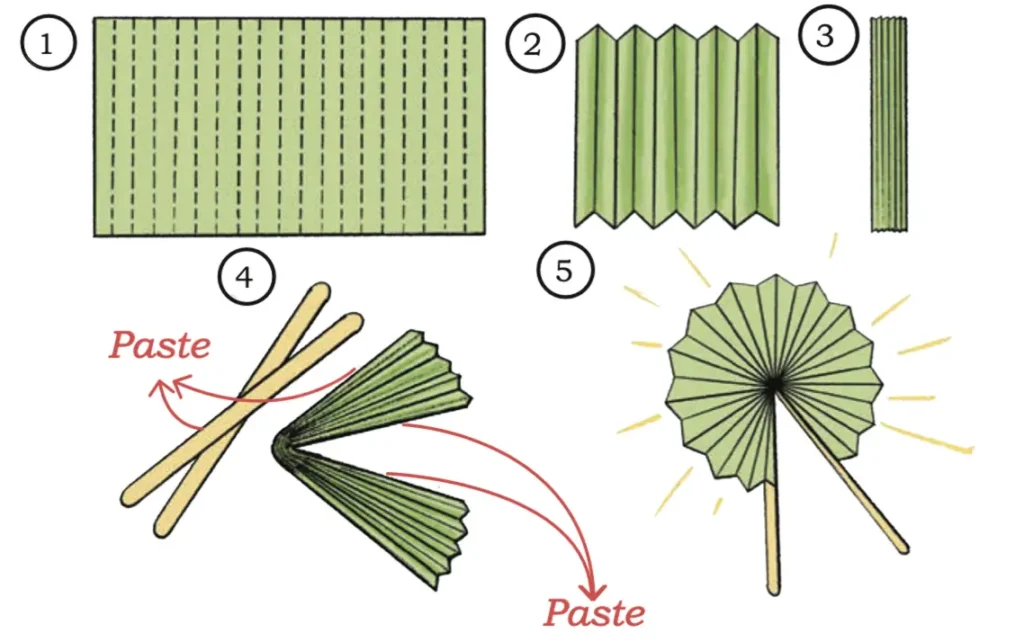
(a) Making a paper fan. Take a rectangular paper, fold every 2 cm as shown in the picture. Paste ice cream sticks as shown below to create a paper fan.

Use your paper fan to show different acute angles and obtuse angles.

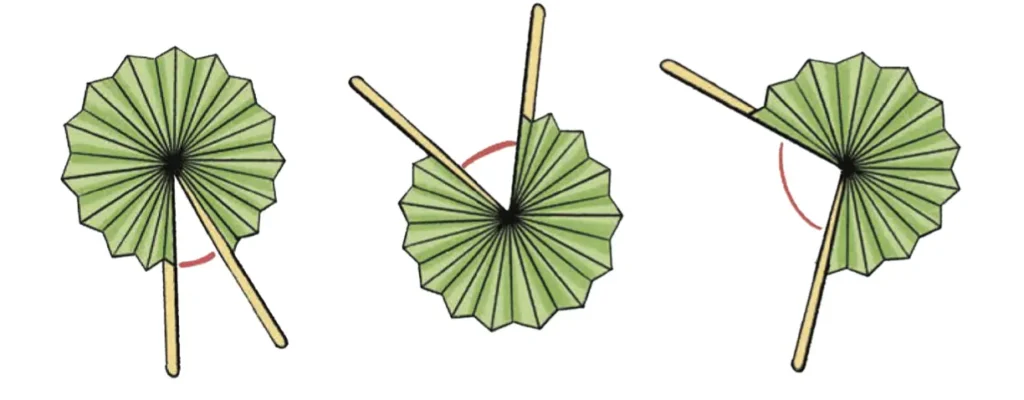
Let us look at the turns made by the paper fan, keeping one side fixed.

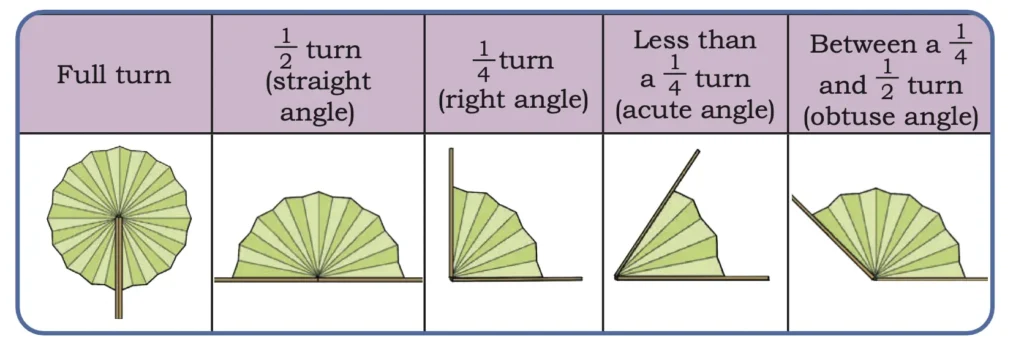
Make an acute turn with the straws or fan. Continue to make another acute turn. Can the two acute turns together make another acute turn?

Solution:
Yes, two acute angles together can make another acute turn. For example, 30° and 45° are two acute angles, and their sum, 30° + 45° = 75,° is also an acute angle.

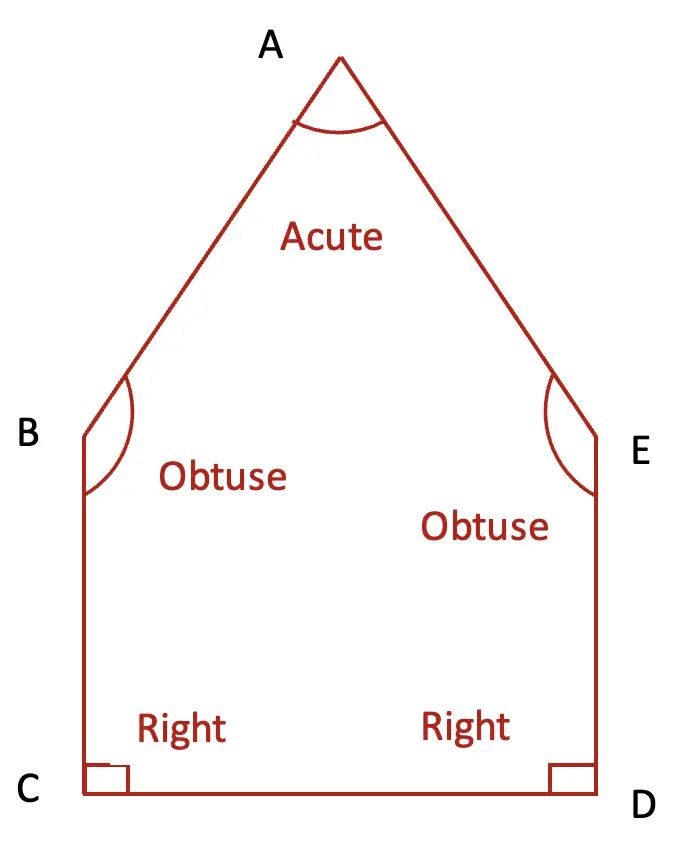
(b) You might have built houses using the hard covers of notebooks or cardboard pieces. Look at the angles marked in the house. What angles are you able to see in this house?

Write your answers as right, acute or obtuse angle.
A: ______________ B: _____________
C: ______________ D: _____________
E: ______________ F: _____________
G: ______________ H: _____________
Solution:
We can see acute, right and obtuse angles in this house.
A: Obtuse angle
B: Right angle
C. Acute angle
D. Acute angle
E. Acute angle
F. Right angle
G. Right angle
H. Obtuse angle

(c) Make a 5-sided shape with 2 right angles, 2 obtuse angles, and 1 acute angle in your notebook.
Solution:

One acute angle: ∠A
Two obtuse angles: ∠B and ∠E
Two right angles: ∠C and ∠D

(d) Look at the angle formation between the legs of these gymnasts. Identify whether the angles are acute, obtuse, right or straight.

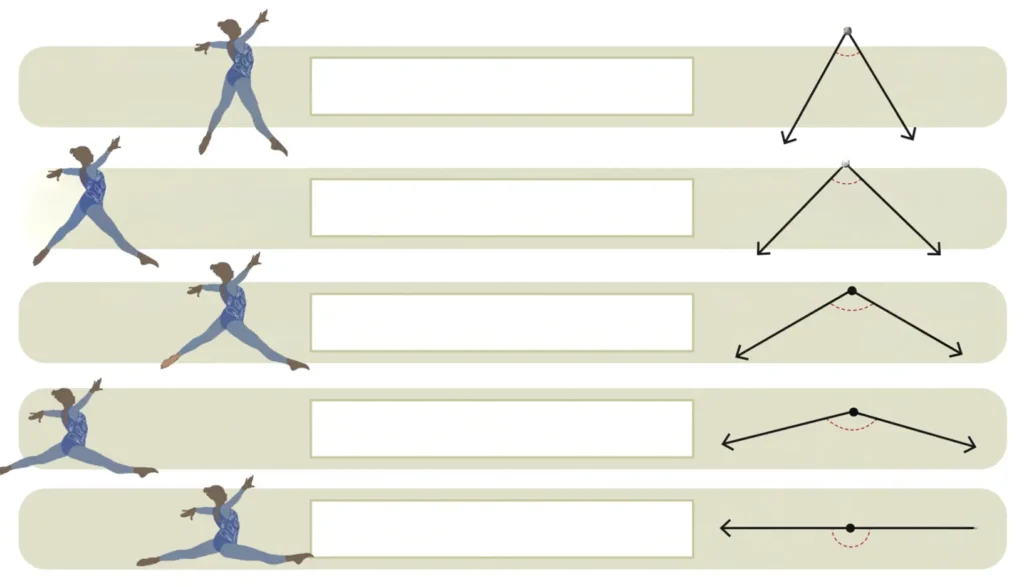
Solution:

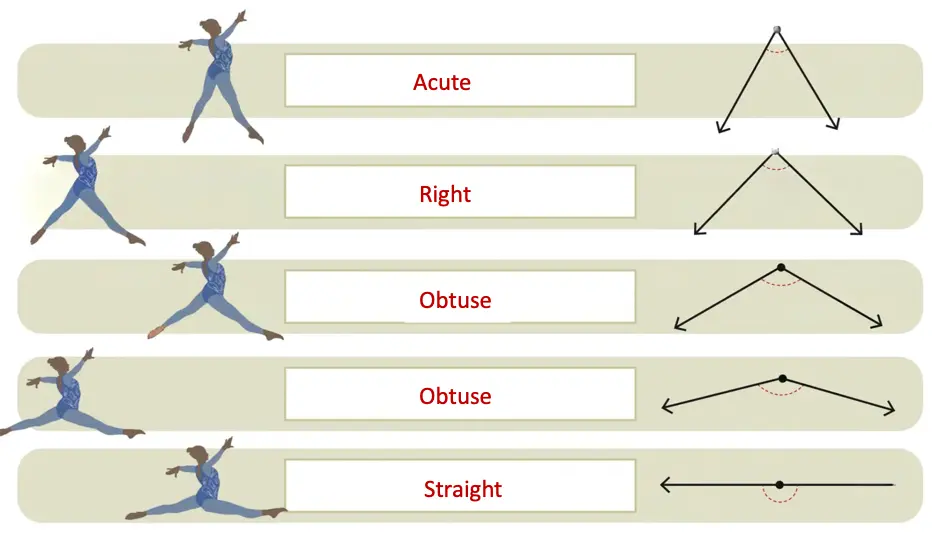
Textbook Page 37

Let Us Think

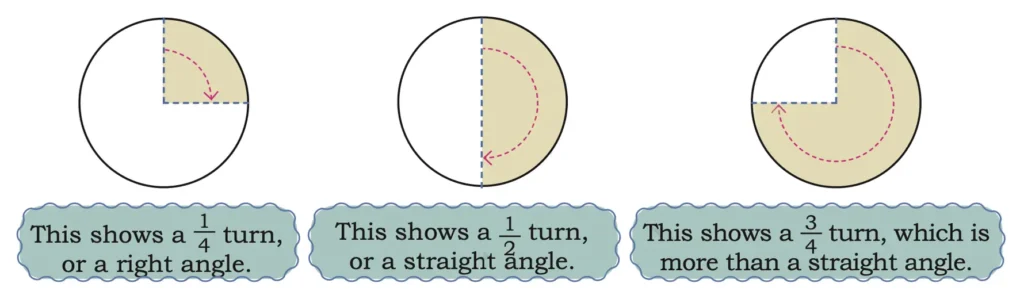
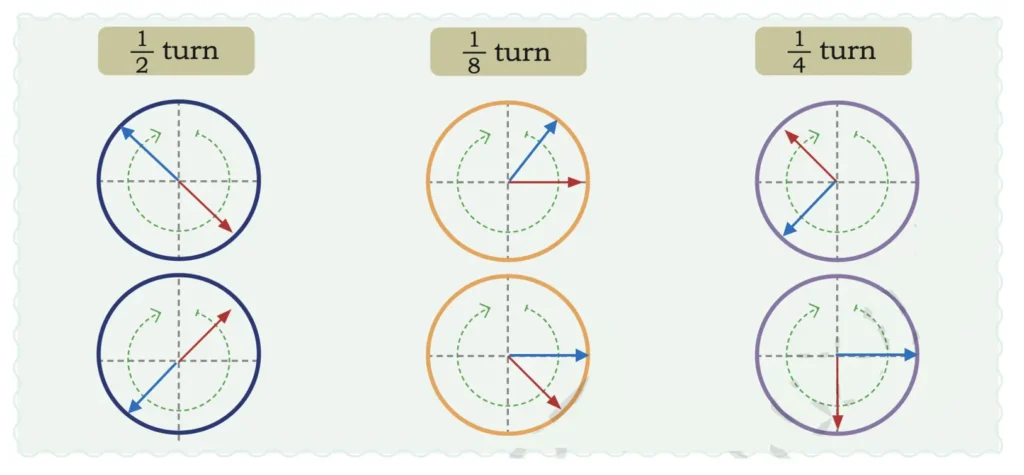
1. In the following circles, the end points of 1/2 , 1/4 , and 1/8 turns are shown. Draw arrows to show the starting points.

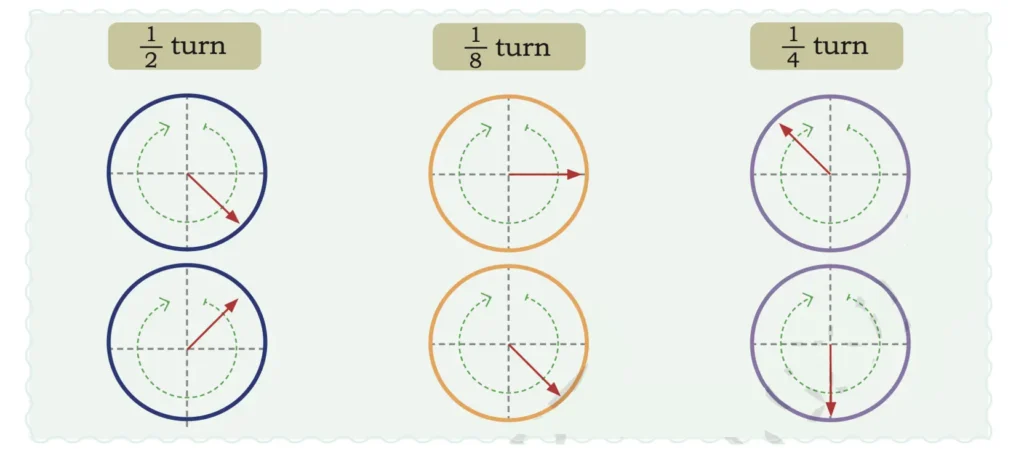
Solution:

Textbook Page 38 – 40

Let Us Do

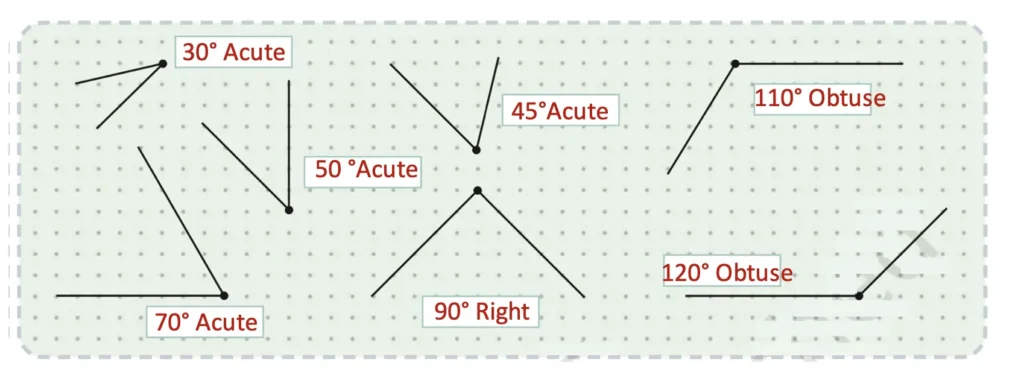
1. Guess the measures of each of the angles shown below. Then, check using your angle measuring tools. You may need to use a combination of measures. Also, state whether each of the angles is acute, right, or obtuse.

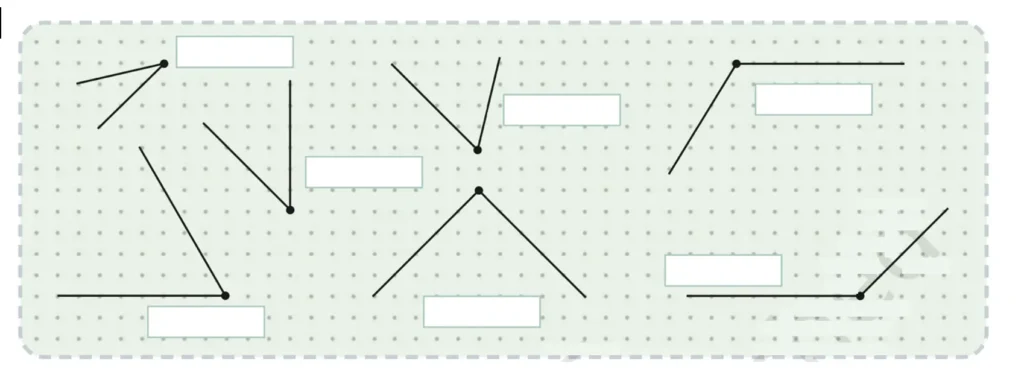
Solution:

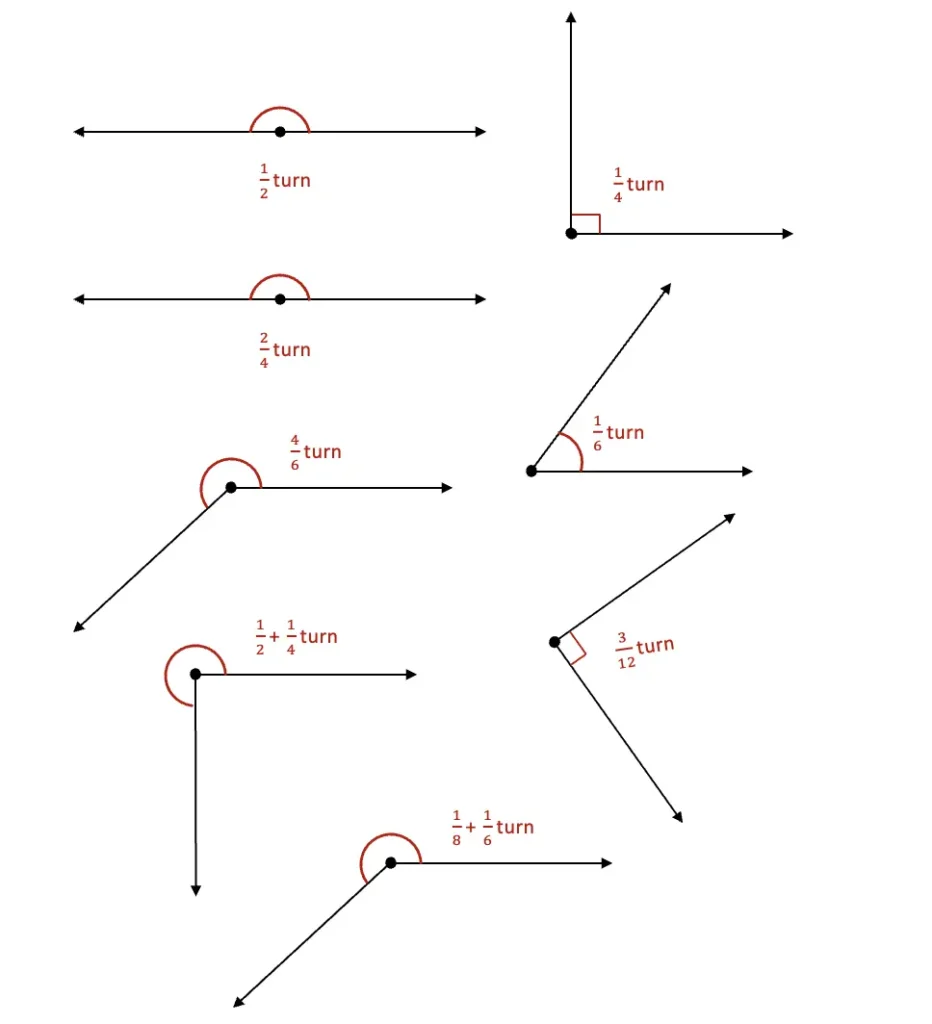
2. Guess the measure of the turns made by the arrow in each of the following cases. Verify with a combination of angle measuring tools.

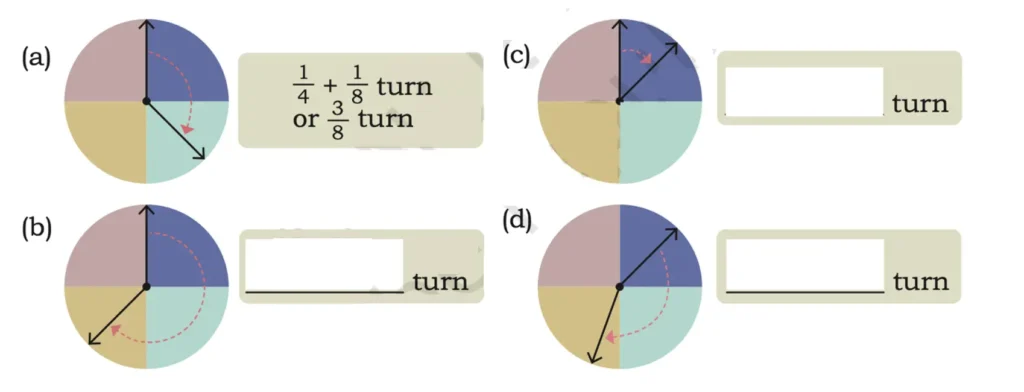
Solution:

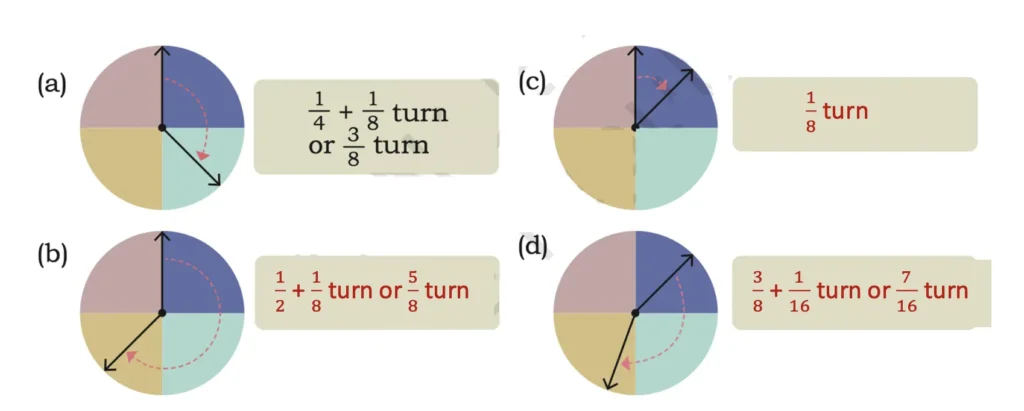
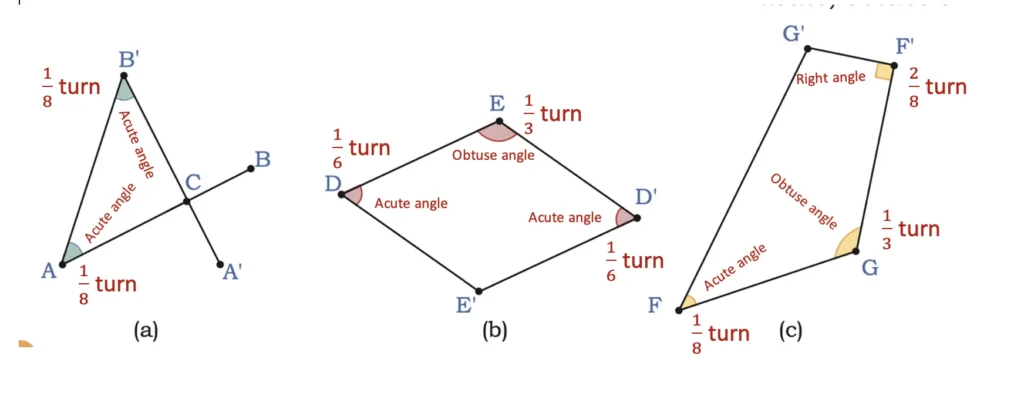
3. Measure each angle in the given shapes. Write the measure of the angles in terms of turns and describe whether they are acute, obtuse or right angles.

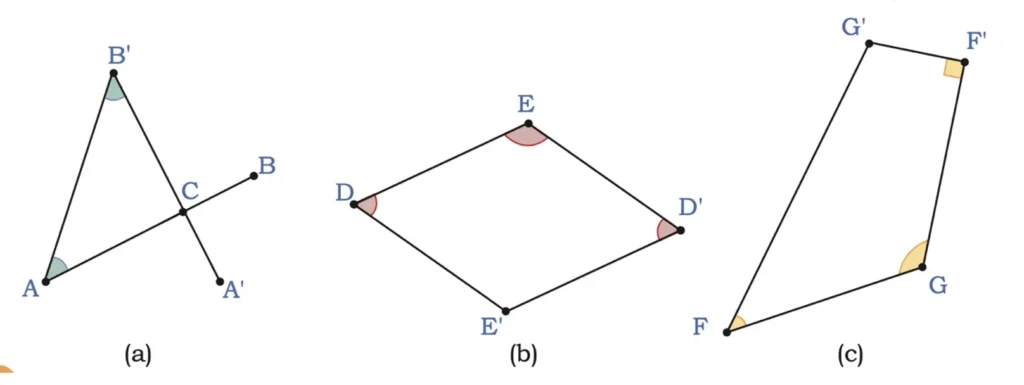
Solution:

4. Draw angles for the given measures of turns using the given lines.

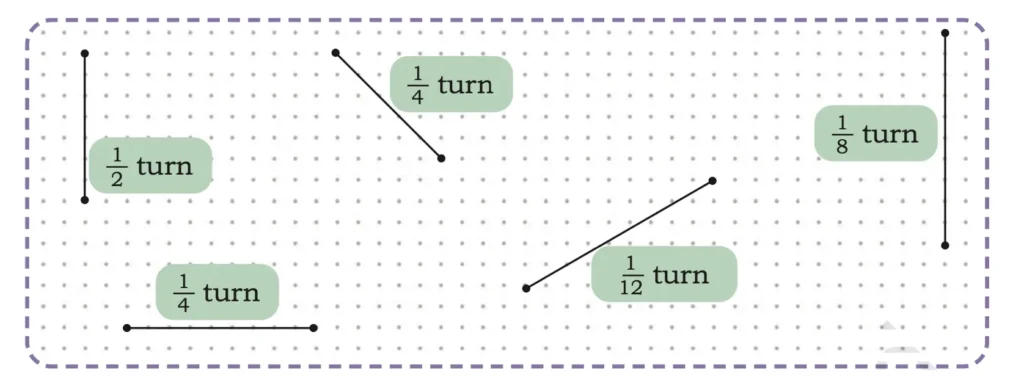
Solution:

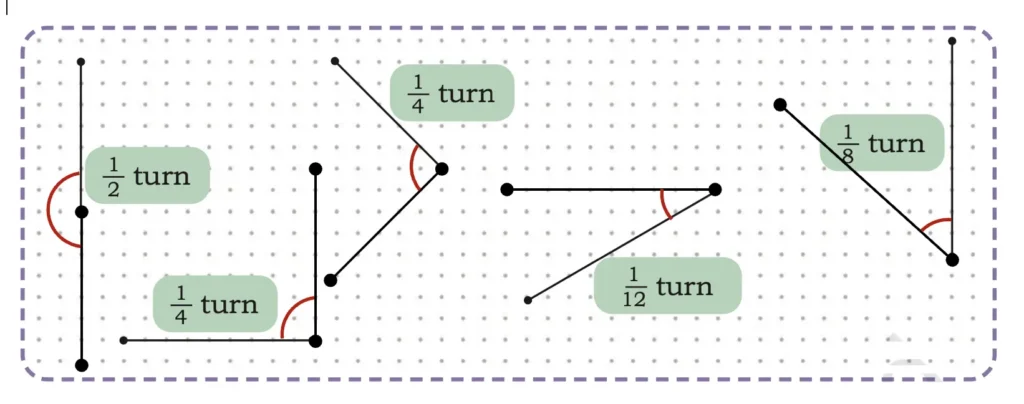
5. Draw the angles formed by the following turns in your notebook.

Solution:

6. Guess the measure of turns the minute hand of a clock makes in each of the following cases. The initial position of the minute hand is given. Draw the final position of the minute hand on the clock face. Discuss your reasoning in class.

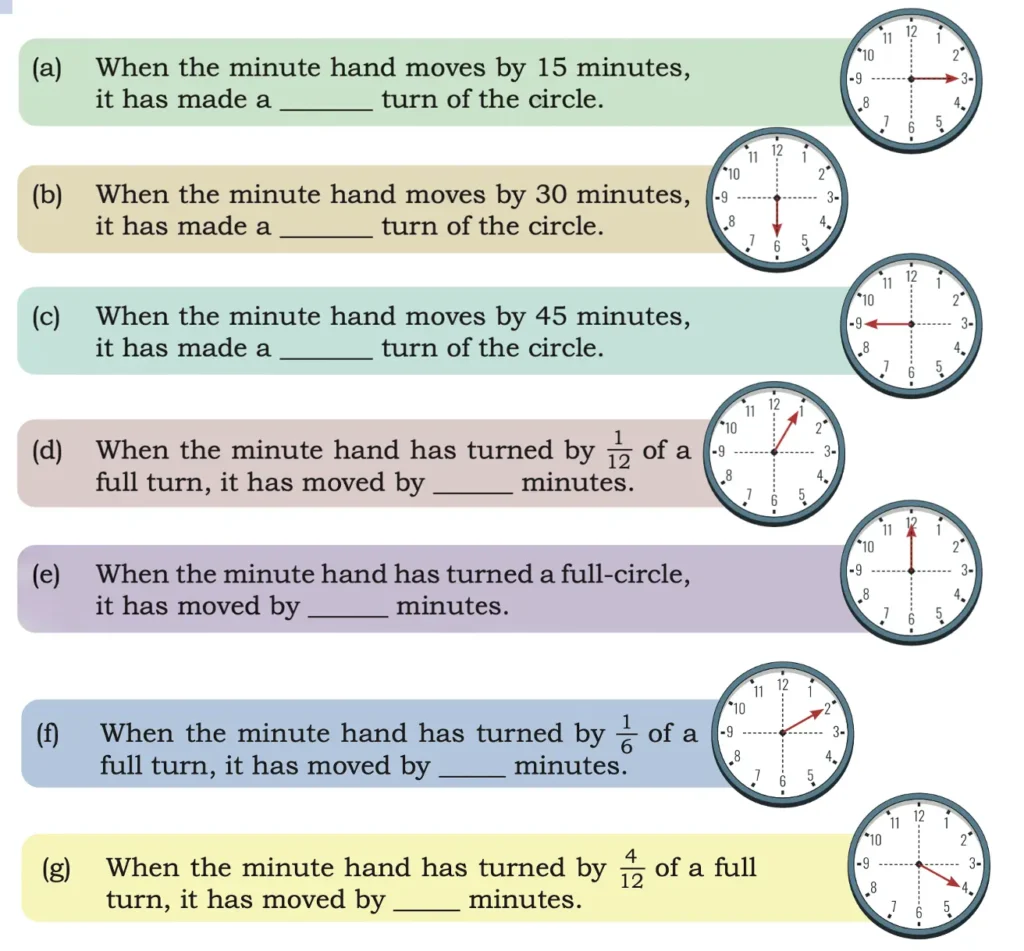
Solution:
(a) 1/4 turn.

(b) 1/2 turn.

(c) 3/4 turn.

(d) 1/12 × 60 = 5 minutes.

(e) 60 minutes.

(f) 1/6 × 60 = 10 minutes.

(g) 4/12 × 60 = 4 × 5 = 20 minutes.

Which direction?

In which direction do the hands of a clock move? The direction in which the hands of the clock move is called clockwise movement. The opposite movement is called anti-clockwise movement.
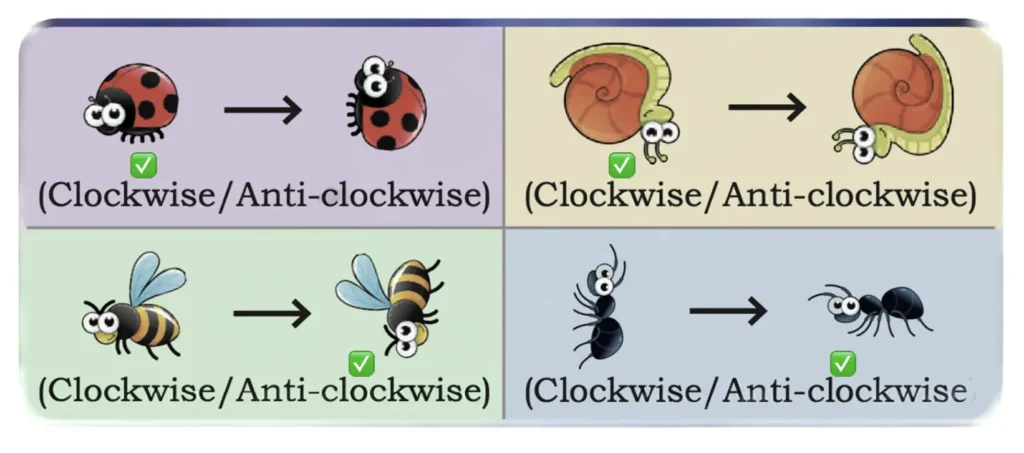
The creatures below have made a quarter turn once. Tick the direction in which they have moved.

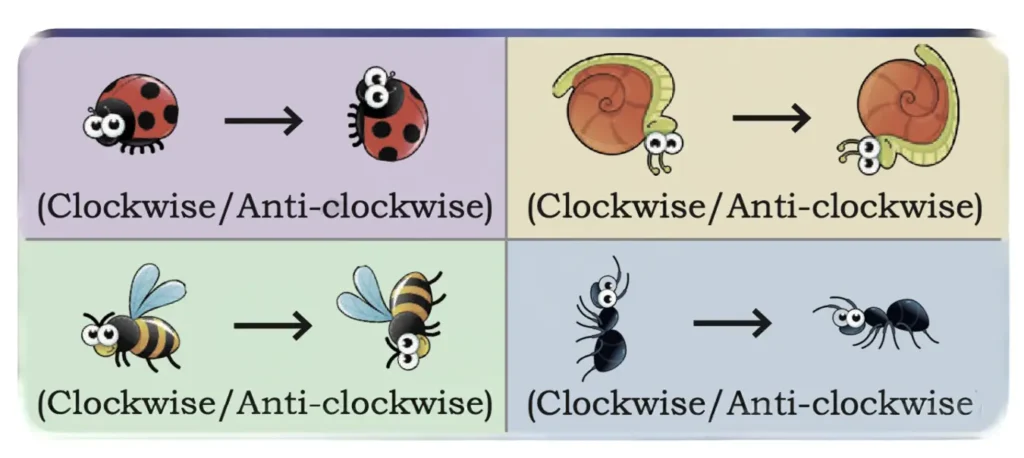
Solution:

Textbook Page 40 – 41

Fun with Turns

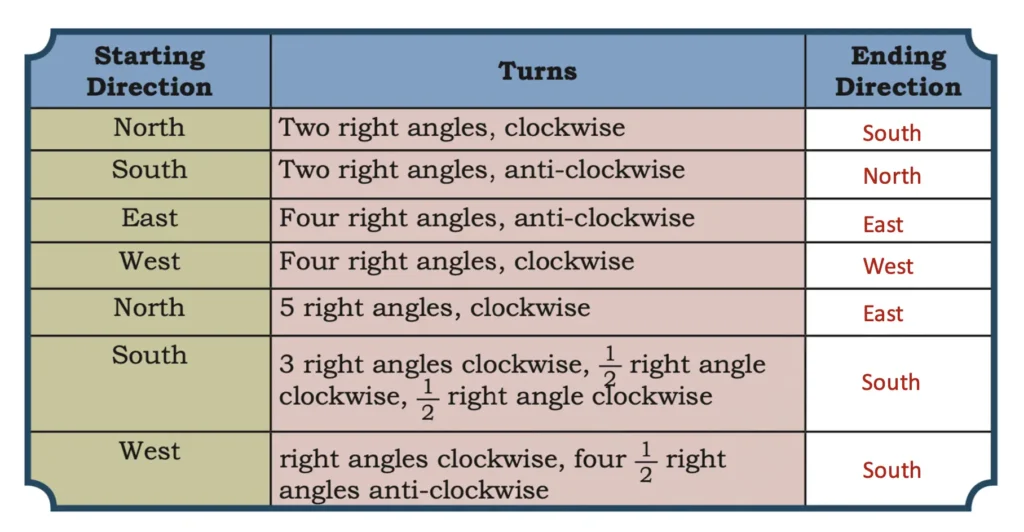
1. The children in a class are playing a game in which the teacher tells them the direction in which they should rotate. Complete the table by filling the direction the children will face on completing the given turns. The starting direction is given in the table.

Solution:

2. Padma is facing the toy shop. What place will she face if she takes a half turn clockwise?
What other way can she turn to face the same place?

Solution:
If she takes a half turn clockwise, she will face the ice cream vendor.
She can take a half turn anticlockwise to face the same place.