Class 8 Maths Chapter 2 Power Play Ganita Prakash NCERT Solutions

Textbook Page 22 – 23

Figure it Out

1. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) y × y
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
Solution:
(i) 6 × 6 × 6 × 6 = 6⁴

(ii) y × y = y²

(iii) b × b × b × b = b⁴

(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³.

(v) 2 × 2 × a × a = 2² × a².

(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d.

2. Express each of the following as a product of powers of their prime factors in exponential form.
(i) 648 (ii) 405 (iii) 540 (iv) 3600
Solution:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2³ × 3⁴.

(ii) 405 = 3 × 3 × 3 × 3 × 5 = 3⁴ × 5.

(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = 2² × 3³ × 5.

(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 2⁴ × 3² × 5².

3. Write the numerical value of each of the following:
(i) 2 × 10³
(ii) 7² × 2³
(iii) 3 × 4⁴
(iv) (-3)² × (-5)²
(v) 3² × 10⁴
(vi) (-2)⁵ × (-10)⁶
Solution:
(i) 2 × 10³
= 2 × (10 × 10 × 10)
= 2 × 1000
= 2000.

(ii) 7² × 2³
= (7 × 7) × (2 × 2 × 2)
= 49 × 8
= 392.

(iii) 3 × 4⁴
= 3 × (4 × 4 × 4 × 4)
= 3 × (16 × 16)
= 3 × 256
= 768.

(iv) 3² × 10⁴
= {(-3) × (-3)} × {(-5) × (-5)}
= 9 × 25
= 225.

(v) 3² × 10⁴
= (3 × 3) × (10 × 10 × 10 × 10)
= 9 × 10000
= 90000.

(vi) (-2)⁵ × (-10)⁶
= {(-2) × (-2) × (-2) × (-2) × (-2)} × {(-10) × (-10) × (-10) × (-10) × (-10) × (-10)}
= {4 × 4 × (-2)} × {100 × 100 × 100}
= (-32) × (1000000)
= -32000000.

Textbook Page 44 – 45

Figure it Out

1. Find out the units digit in the value of 2²²⁴ ÷ 4³² ?
Solution:
2²²⁴ ÷ 4³²
= 2²²⁴ ÷ (2²)³²
= 2²²⁴ ÷ 2^{2 × 32}
= 2²²⁴ ÷ 2⁶⁴
= 2^{224 – 64} = 2¹⁶⁰

2¹ = 2 (units digit 2)
2² = 4 (units digit 4)
2³ = 8 (units digit 8)
2⁴ = 16 (units digit 6)
2⁵ = 32 (units digit 2)
2⁶ = 64 (units digit 4)
2⁷ = 128 (units digit 8)
………..
………..
Here, the pattern repeats after every 4 steps.
So, the unit’s digit of 2¹⁶⁰ is the same as that of 2⁴, which is 6.

2. There are 5 bottles in a container. Every day, a new container is brought in. How many bottles would be there after 40 days?
Solution:
Number of containers added every day = 1
Number of containers after 40 days = 40 containers
Number of bottles in a container = 5
Total bottles in 40 containers = 5 × 40 = 200 bottles
Therefore, there would be 200 bottles after 40 days.

3. Write the given number as the product of two or more powers in three different ways. The powers can be any integers.
(i) 64³
(ii) 192⁸
(iii) 32^-5
Solution:
(i) 64³
64 = 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
64³ = (2⁶)³ = 2¹⁸
Three different ways:
1. 64³ = 2¹⁸ = 2⁹ × 2⁹
2. 64³ = 2¹⁸ = 2¹⁰ × 2⁸
3. 64³ = 2¹⁸ = 2⁶ × 2⁶ × 2⁶

(ii) 192⁸
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁶ × 3
192⁸ = (2⁶ × 3)⁸ = 2^{6 × 8} × 3⁸ = 2⁴⁸ × 3⁸
Three different ways:
1. 192⁸ = 2⁴⁸ × 3⁸ = 2⁴⁰ × 2⁸ × 3⁸ = 2⁴⁰ × (2×3)⁸ = 2⁴⁰ × 6⁸
2. 192⁸ = 2⁴⁸ × 3⁸ = (2²⁴×3⁴)×(2²⁴×3⁴)
3. 192⁸ = 2⁴⁸ × 3⁸ = (2⁶)⁸ × 3⁸

(iii) 32^-5
32 = 2 × 2 × 2 × 2 × 2 = 2⁵
32^-5 = (2⁵)^-5 = 2^-25
Three different ways:
1. 32^-5 = 2^-25 = 2^-15 × 2^-10
2. 32^-5 = 2^-25 = 2⁻⁵ × 2⁻⁵ × 2⁻⁵ × 2⁻⁵ × 2⁻⁵
3. 32^-5 = 2^-25 = 2^-5 × 2^-20

4. Examine each statement below and find out if it is ‘Always True’, ‘Only Sometimes True’, or ‘Never True’. Explain your reasoning.
(i)  Cube numbers are also square numbers.
(ii)  Fourth powers are also square numbers.
(iii)  The fifth power of a number is divisible by the cube of that number.
(iv)  The product of two cube numbers is a cube number.
(v)  q46 is both a 4th power and a 6th power (q is a prime number).
Solution:
(i) Only sometimes true.
Explanation: 64 = 2⁶ = (2³)² = (2²)³ is both a cube and a square.
But 8 = 2³ is a cube, not a square.

(ii) Always true.
Eplanation: 3⁴ = (3²)² = 9².
5⁴ = (5²)² = 25².

(iii) Always true.
Explanation: a⁵ = a³ × a² and is divisible by a³.

(iv) Always true.
Explanation: 8 = 2³, 27 = 3³
8 × 27 = 216, which is 6³.

(v) Never true.
Explanation: Since 46 is not divisible by 4 or 6. Therefore, there is no prime number q such that q⁴⁶ is both a perfect fourth power and a perfect sixth power. 

5. Simplify and write these in the exponential form.
(i) 10^–2 × 10^–5
(ii) 5⁷ ÷ 5⁴
(iii) 9^–7 ÷ 9⁴
(iv) (13^–2)^–3
(v) m⁵n¹²(mn)⁹
Solution:
(i) 10^–2 × 10^–5 = 10^{-2 – 5} = 10^-7

(ii) 5⁷ ÷ 5⁴ = 5^{7 – 4} = 5³

(iii) 9^–7 ÷ 9⁴ = 9^{-7 + 4} = 9^–3

(iv) (13^–2)^–3 = 13^{-2 × -3} = 13⁶

(v) m⁵n¹²(mn)⁹ = m⁵n¹² × m⁹n⁹ = m⁵⁺⁹n¹²⁺⁹ = m¹⁴n²¹

6. If 12² = 144 what is
(i) (1.2)²
(ii) (0.12)²
(iii) (0.012)²
(iv) 120²
Solution:

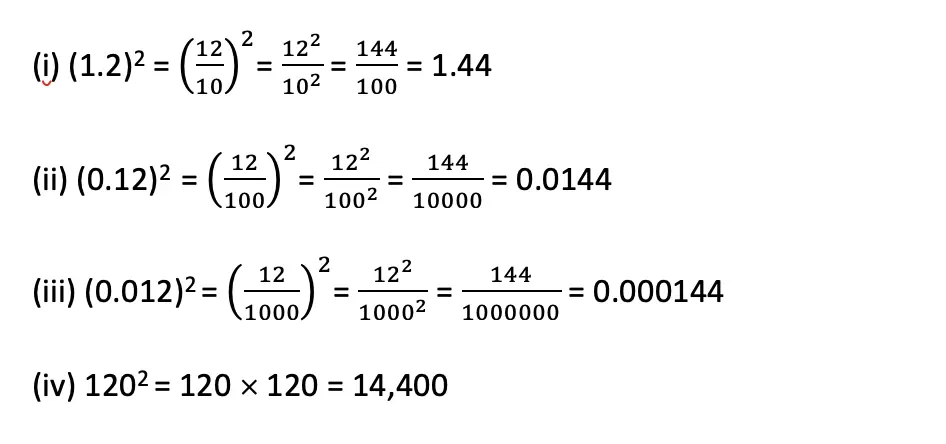
7. Circle the numbers that are the same —
2⁴ × 3⁶, 6⁴ × 3², 6¹⁰, 18² × 6², 6²⁴
Solution:
(i) 2⁴ × 3⁶

(ii) 6⁴ × 3² = (2 × 3)⁴ × 3² = 2⁴ × 3⁴ × 3² = 2⁴ × 3⁶

(iii) 6¹⁰ = (2 × 3)¹⁰ = 2¹⁰ × 3¹⁰

(iv) 18² × 6² = (2 × 3 × 3)² × (2 × 3)² = 2² × 3² × 3² × 2² × 3² = 2⁴ × 3⁶

(v) 6²⁴ = (2 × 3)²⁴ = 2²⁴ × 3²⁴

Therefore, 2⁴ × 3⁶, 64 × 32, and 18² × 6² are the same.

8. Identify the greater number in each of the following —
(i) 4³ or 3⁴ (ii) 2⁸ or 8² (iii) 100² or 2¹⁰⁰
Solution:
(i) 4³ or 3⁴
4³ = 64 , 3⁴ = 81
So, 3⁴ is greater.

(ii) 2⁸ or 8²
2⁸ = 256, 8² = 64
So, 2⁸ is greater.

(iii) 100² or 2¹⁰⁰
100² = 10,000
2¹⁰⁰ = (2¹⁰)¹⁰ = 1024¹⁰, which is far greater than 10,000.
So, 2¹⁰⁰ is greater than 100².

9. A dairy plans to produce 8.5 billion packets of milk in a year. They want a unique ID (identifier) code for each packet. If they choose to use the digits 0–9, how many digits should the code consist of?
Solution:
8.5 billion = 8,500,000,000

Therefore, the code should contain at least 10 digits to get a unique ID for each packet.

10. 64 is a square number (8²) and a cube number (4³). Are there other numbers that are both squares and cubes? Is there a way to describe such numbers in general?
Solution:
Yes, there are other numbers that are both squares and cubes. For example:
729 = 9³ (cube number) = 27² (perfect square)
4096 = 16³ (cube number) = 64² (perfect square)
General Rule: The sixth power of any number (i.e., n⁶) is both a square and a cube. i.e.
1⁶ = 1
2⁶ = 64
3⁶ = 729
4⁶ = 4096
5⁶ = 15,625

11. A digital locker has an alphanumeric (it can have both digits and letters) passcode of length 5. Some example codes are G89P0, 38098, BRJKW, and 003AZ. How many such codes are possible?
Solution:
Length of passcode = 5
Total choices of alphabets and letters for each slot = 26 + 10 = 36
Total possible codes = 36 × 36 × 36 × 36 × 36 = 36⁵

12. The worldwide population of sheep (2024) is about 10⁹, and that of goats is also about the same. What is the total population of sheep and goats?
(i) 20⁹ (ii) 10¹¹ (iii) 10¹⁰
(iv) 10¹⁸ (v) 2 × 10⁹ (vi) 10⁹ + 10⁹
Solution:
Population of sheep = 10⁹
Population of goats = 10⁹
Total population of sheep and goats = 10⁹ + 10⁹ or 2 × 10⁹
Therefore, (v) 2 × 10⁹ and (vi) 10⁹ + 10⁹ are the correct answers.

13. Calculate and write the answer in scientific notation:
(i)  If each person in the world had 30 pieces of clothing, find the total number of pieces of clothing.
(ii)  There are about 100 million bee colonies in the world. Find the number of honeybees if each colony has about 50,000 bees.
(iii)  The human body has about 38 trillion bacterial cells. Find the bacterial population residing in all humans in the world.
(iv) Total time spent eating in a lifetime in seconds.
Solution:
(i) Estimated world population: ≈ 8 billion = 8 × 10⁹
Number of pieces of clothing each person had = 30 pieces
Total number of pieces of clothing = 8×10⁹ × 30 = 2.4 × 10¹¹

(ii) Number of bee colonies in the world = 100 million = 1×10⁸
Number of bees in each colony = 50,000 = 5 × 10⁴
Total number of honeybees = 1 × 10⁸ × 5 × 10⁴ = 5 × 10¹²

(iii) World population ≈ 8 × 10⁹
Number of bacterial cells in human body = 38 trillion = 3.8 × 10¹³
Total bacterial population residing in all humans in the world = (3.8 × 10¹³)× (8 × 10⁹) = 30.4 × 10²² = 3.04 × 10²³

(iv) Average person’s lifespan = 80 years
Time spent eating daily = 1.5 hours
Total eating time per day in seconds = 1.5 × 3600 = 5400 seconds
Number of days in 80 years = 80 × 365 = 29,200
Total seconds spent eating in a lifetime in seconds = 5400 × 29,200 = 1.5768 × 10⁸

14. What was the date 1 arab/1 billion seconds ago?
Solution:
1 billion seconds = 1,000,000,000 seconds
1,000,000,000 ÷ (60 × 60 × 24 × 365) = 31.71 years
31.71 years = 31 full years and 0.71 × 365 = 259 days
Today is: 28 July 2025
Subtracting 31 years → 28 July 1994
Going back 259 days from 28 July 1994 → 11 November 1993.
So, 1 billion seconds ago was November 11, 1993.