Class 8 Maths Ganita Prakash Chapter 2 Power Play NCERT Solutions

Class 8 Maths Ganita Prakash Chapter 2 Power Play NCERT Solutions helps you master the exciting world of exponents and powers. This chapter simplifies large numbers and teaches effective methods for multiplying and dividing them. Get clear, step-by-step solutions to every question and boost your confidence!

Textbook Page 20

The following table lists the thickness after each fold. Observe that the thickness doubles after each fold.

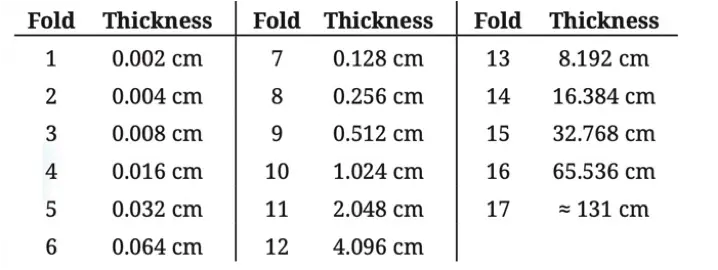
(We use the sign ‘≈’ to indicate ‘approximately equal to’.)
After 10 folds, the thickness is just above 1 cm (1.024 cm). After 17 folds, the thickness is about 131 cm (a little more than 4 feet).

Q. Now, what do you think the thickness would be after 30 folds? 45 folds? Make a guess.
Solution:
I think that the thickness after 30 folds would be 10 km, and after 45 folds it would be 20,000 km.

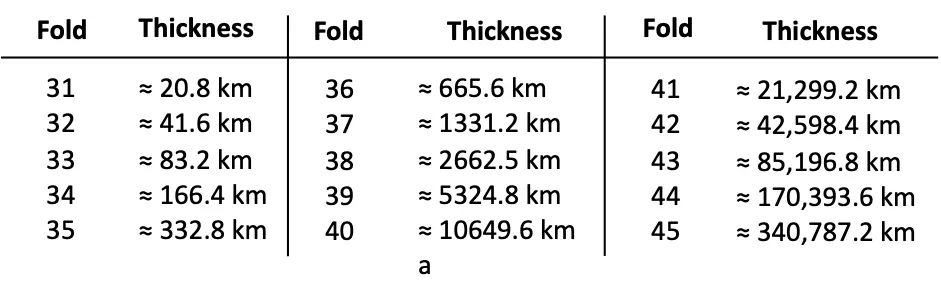
Q. Fill the table below.

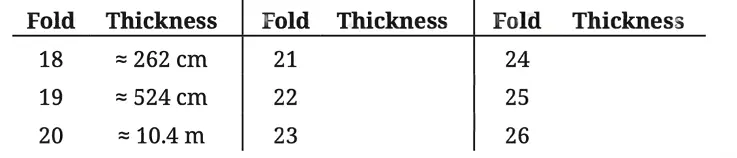
Solution:

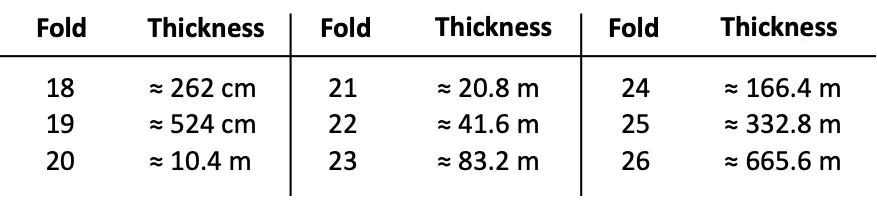
Q. After 26 folds, the thickness is approximately 670 m. Burj Khalifa in Dubai, the tallest building in the world, is 830 m tall.

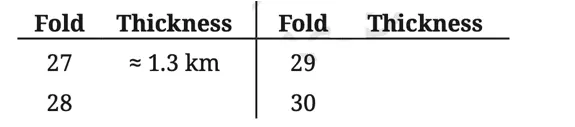
Solution:

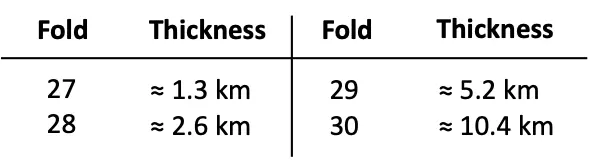
Q. After 30 folds, the thickness of the paper is about 10.7 km, the typical height at which planes fly. The deepest point discovered in the oceans is the Mariana Trench, with a depth of 11 km.

Solution:

Textbook Page 22

Q. Which expression describes the thickness of a sheet of paper after it is folded 10 times? The initial thickness is represented by the letter-number v.
(i) 10v       (ii) 10 + v        (iii) 2 × 10 × v
(iv) 2¹⁰  (v) 2¹⁰v           (vi) 10²v
Solution:
Initial thickness of sheet = v
Since the thickness of the sheet doubles after every fold.
Thus, after 10 folds, the thickness of a sheet of paper = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × v = 2¹⁰v.
Therefore, (v) 2¹⁰v  is the correct answer.

Q. What is (-1)⁵? Is it positive or negative? What about (-1)⁵⁶ ?
Solution:
(-1)^odd = −1 → Negative
(-1)^even = 1 → Positive
(i) (-1)⁵
Since 5 is an odd number, (-1)⁵ = -1, which is negative.

(ii) (-1)⁵⁶
Since 56 is an even number, (-1)⁵⁶ = 1, which is positive.

Q. Is (-2)⁴ = 16? Verify.
Solution:
(-2)⁴ = (-2) × (-2) × (-2) × (-2)
(-2)⁴ = (-2) × (-2) × (-2) × (-2)
(-2)⁴ = 4 × 4
(-2)⁴ = 16.
So yes, (-2)⁴ = 16 is correct.

Q. What is 0², 0⁵? What is 0ⁿ?
Solution:
0² = 0 × 0 = 0.
0⁵ = 0 × 0 × 0 × 0 × 0 = 0.
Similarly, 0ⁿ = 0.

Textbook Page 22 – 23

Figure it Out

1. Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) y × y
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
Solution:
(i) 6 × 6 × 6 × 6 = 6⁴

(ii) y × y = y²

(iii) b × b × b × b = b⁴

(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³.

(v) 2 × 2 × a × a = 2² × a².

(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d.

2. Express each of the following as a product of powers of their prime factors in exponential form.
(i) 648 (ii) 405 (iii) 540 (iv) 3600
Solution:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2³ × 3⁴.

(ii) 405 = 3 × 3 × 3 × 3 × 5 = 3⁴ × 5.

(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = 2² × 3³ × 5.

(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 2⁴ × 3² × 5²

3. Write the numerical value of each of the following:
(i) 2 × 10³
(ii) 7² × 2³
(iii) 3 × 4⁴
(iv) (-3)² × (-5)²
(v) 3² × 10⁴
(vi) (-2)⁵ × (-10)⁶
Solution:
(i) 2 × 10³
= 2 × (10 × 10 × 10)
= 2 × 1000
= 2000.

(ii) 7² × 2³
= (7 × 7) × (2 × 2 × 2)
= 49 × 8
= 392.

(iii) 3 × 4⁴
= 3 × (4 × 4 × 4 × 4)
= 3 × (16 × 16)
= 3 × 256
= 768.

(iv) 3² × 10⁴
= {(-3) × (-3)} × {(-5) × (-5)}
= 9 × 25
= 225.

(v) 3² × 10⁴
= (3 × 3) × (10 × 10 × 10 × 10)
= 9 × 10000
= 90000.

(vi) (-2)⁵ × (-10)⁶
= {(-2) × (-2) × (-2) × (-2) × (-2)} × {(-10) × (-10) × (-10) × (-10) × (-10) × (-10)}
= {4 × 4 × (-2)} × {100 × 100 × 100}
= (-32) × (1000000)
= -32000000.

Textbook Page 24

Q. 3⁷ can also be written as 3² × 3⁵. Can you reason out why?
Solution:
Yes, 3⁷ can also be written as 3² × 3⁵ because 3⁷ = (3 × 3) × (3 × 3 × 3 × 3 × 3), which becomes 3² × 3⁵.

Q. n^a × n^b = n^(a+b), where a and b are counting numbers.
Use this observation to compute the following.
(i) 2⁹
(ii) 5⁷
(iii) 4⁶
Solution:
(i) 2⁹ = (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) = 2³ × 2³ × 2³ = 8 × 8 × 8 = 512.

(ii) 5⁷ = (5 × 5) × (5 × 5) × (5 × 5) × 5 = 5² × 5² × 5² × 5 = 25 × 25 × 25 × 5 = 78,125.

(iii) 4⁶ = (4 × 4) × (4 × 4) × (4 × 4) = 4² × 4² × 4² = 16 × 16 × 16 = 4096.

Q. Write the following expressions as a power of a power in at least two different ways:
(i) 8⁶
(ii) 7¹⁵
(iii) 9¹⁴
(iv) 5⁸
Solution:
(i) 8⁶
Two possible ways:
8⁶ = (8³)²
8⁶ = (8²)³

(ii) 7¹⁵
Two possible ways:
7¹⁵ = (7³)⁵
7¹⁵ = (7⁵)³

(iii) 9¹⁴
Two possible ways:
9¹⁴ = (9²)⁷
9¹⁴ = (9⁷)²

(iv) 5⁸
Two possible ways:
5⁸ = (5²)⁴
5⁸ = (5⁴)²

Textbook Page 25

In the middle of a beautiful, magical pond lies a bright pink lotus. The number of lotuses doubles every day in this pond. After 30 days, the pond is completely covered with lotuses. On which day was the pond half full?
If the pond is completely covered by lotuses on the 30th day, how much of it is covered by lotuses on the 29th day?
Since the number of lotuses doubles every day, the pond should be half covered on the 29th day.

Q. Write the number of lotuses (in exponential form) when the pond was —
(i) fully covered (ii) half covered
Solution
The number of lotuses doubles every day.
On the 30th day, the pond is fully covered.
So, on the 29th day, the pond must be half full.
Number of lotuses:
Day 1 → 1 = 2⁰
Day 2 → 2¹
Day 3 → 2²
Day 4 → 2³
…….
Day 29 → 2²⁸
Day 30 → 2²⁹
(i) The number of lotuses when the pond was fully covered (Day 30) = 2²⁹.
(ii) The number of lotuses when the pond was fully covered (Day 29) = 2²⁸.

Q. m^a × n^a = (mn)^a, where a is a counting number.
Use this observation to compute the value of 2⁵ × 5⁵.
Solution:
2⁵ × 5⁵ = (2 × 5)⁵ = (10)⁵.

Q. Simplify 10⁴/5⁴ and write it in exponential form.
Solution:

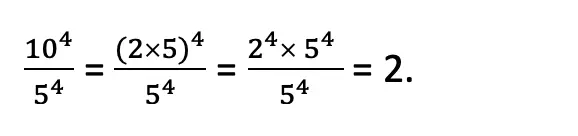
Textbook Page 26

How Many Combinations

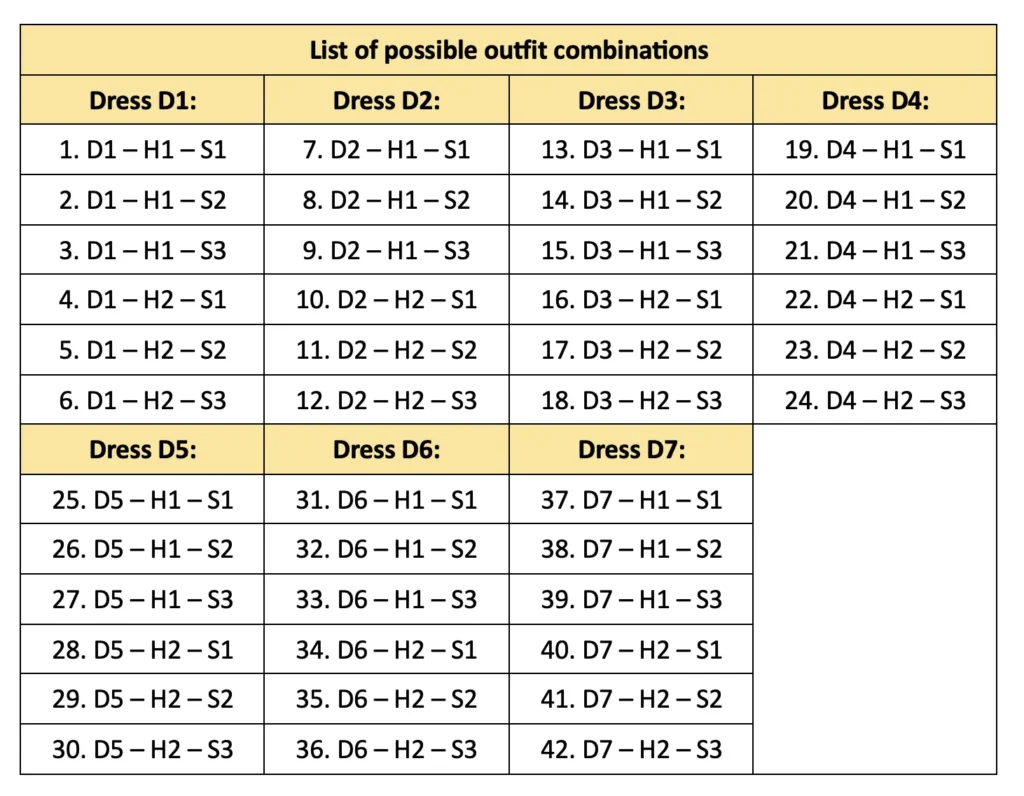
Q. Roxie has 7 dresses, 2 hats, and 3 pairs of shoes. How many different ways can Roxie dress up?
Hint: Try drawing a diagram like the one above.
Solution:
Each outfit includes one dress, one hat, and one pair of shoes.
Dresses: D1, D2, D3, D4, D5, D6, D7
Hats: H1, H2
Shoes: S1, S2, S3
Total combination of outfits = 7 × 2 × 3 = 42.

Textbook Page 27

Q. Estu says, “Next time, I will buy a lock that has 6 slots with the letters A to Z. I feel it is safer.”
How many passwords are possible with such a lock?
Solution:
Choices of letters for each slot = 26.
Total possible password combinations of a lock with 6 slots = 26 × 26 × 26 × 26 × 26 × 26 = 26⁶.

Q. What is 2¹⁰⁰ ÷ 2²⁵ in powers of 2?
Solution:

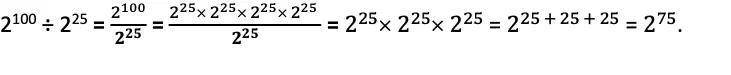
Textbook Page 29

Q. Consider the following general forms we have identified.
n^a × n^b = n^{a + b}
(n^a)^b = (n^b)^a = n^{a × b}
n^a ÷ n^b = n^{a – b}
We had required a and b to be counting numbers. Can a and b be any integers? Will the generalised forms still hold true?
Solution:
Yes, the generalised forms are valid for all integers a and b, as long as the base n ≠ 0.
For example:
n^a × n^-b = n^{a + (-b)} = n^{a – b}
(n^a)^-b = (n^-b)^a = n^{a × (-b)}
n^-a ÷ n^b = n^{-a – b}

Q. Write equivalent forms of the following.
(i) 2^-4
(ii) 10^-5
(iii) (-7)^–2
(iv) (-5)^–3
(v) 10^-100
Solution:

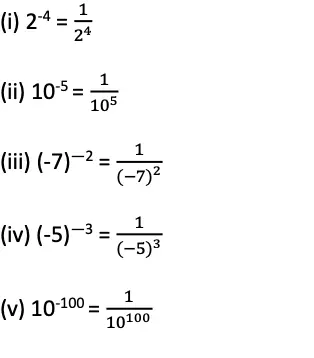
Q. Simplify and write the answers in exponential form.
(i) 2^-4 × 2⁷
(ii) 3² × 3^-5 × 3⁶
(iii) p³ × p^-10
(iv) 2⁴ × (-4)^–2
(v) 8^p × 8^q
Solution:

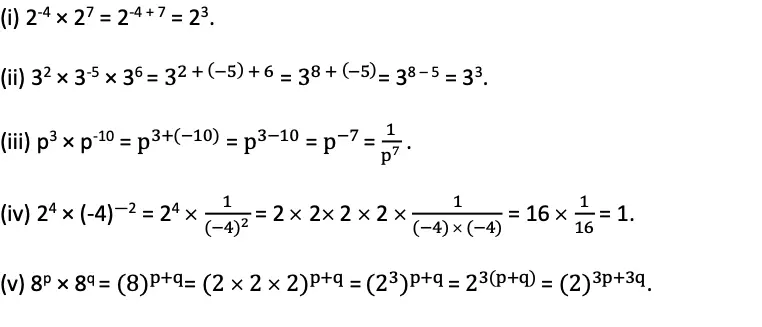
Textbook Page 30

Power Lines

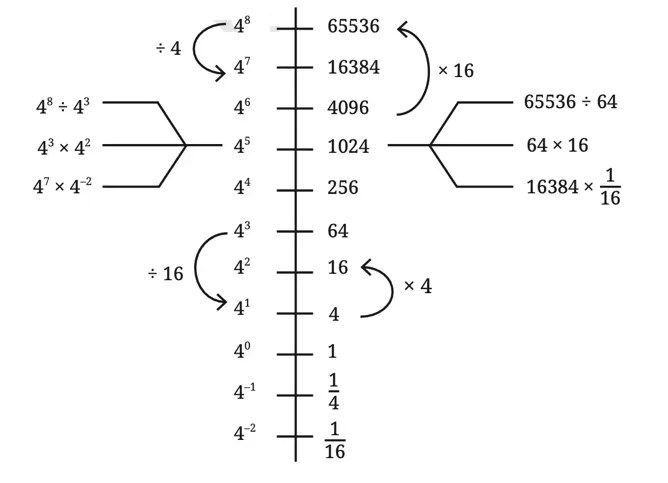
Q. How many times larger than 4^-2 is 4² ?
Solution:
Since, 4² ÷ 4^-2 = 4⁴.
Therefore, 4² is 256 (4⁴) times larger than 4^-2.

Q. Use the power line for 7 to answer the following questions.

Solution:
2401 × 49 = 7⁴ × 7² = 7^{4 + 2} = 7⁶.
49³ = (7²)³ = 7^{2 × 3} = 7⁶.
343 × 2401 = 7³ × 7⁴ = 7^{3 + 4} = 7⁷.

Powers of 10

We have used numbers like 10, 100, 1000, and so on when writing Indian numerals in an expanded form. For example:
47561 = (4 × 10000) + (7 × 1000) + (5 × 100) + (6 × 10) + 1.
This can be written using powers of 10 as
47561 = (4 × 10⁴) + (7 × 10³) + (5 × 10²) + (6 × 10¹) + (1 × 10⁰).

Q. Write these numbers in the same way: (i) 172, (ii) 5642, (iii) 6374.
Solution:
(i) 172 = (1 × 100) + (7 × 10) + 2 = (1 × 10²) + (7 × 10¹) + (2 × 10⁰).
(ii) 5642 = (5 × 1000) + (6 × 100) + (4 × 10) + 2 = (5 × 10³) + (6 × 10²) + (4 × 10¹) + (2 × 10⁰).
(iii) 6374 = (6 × 1000) + (3 × 100) + (7 × 10) + 4 = (6 × 10³) + (3 × 10²) + (7 × 10¹) + (4 × 10⁰).

Textbook Page 32

The distance between the Sun and Saturn is 14,33,50,00,00,000 m = 1.4335 × 10¹² m.
The distance between Saturn and Uranus is 14,39,00,00,00,000 m = 1.439 × 10¹² m.
The distance between the Sun and Earth is 1,49,60,00,00,000 m = 1.496 × 10¹¹ m.
Q. Can you say which of the three distances is the smallest?

Solution:
Since, 10¹¹ < 10¹².
Therefore, the distance between the Sun and Earth is the smallest.

Q. The number line below shows the distance between the Sun and Saturn (1.4335 × 10¹² m). On the number line below, mark the relative position of the Earth. The distance between the Sun and the Earth is 1.496 × 10¹¹ m.

Solution:

Q. Express the following numbers in standard form.
(i) 59,853
(ii) 65,950
(iii) 34,30,000
(iv) 70,04,00,00,000
Solution:
(i) 59,853 = 5.9853 × 10⁴.
(ii) 65,950 = 6.595 × 10⁴.
(iii) 34,30,000 = 3.43 × 10⁶.
(iv) 70,04,00,00,000 = 7.004 × 10¹⁰.

Textbook Page 34

Q. Roxie wonders, “Instead of jaggery if we use 1-rupee coins, how many coins are needed to equal my weight?”. How can we find out?
For questions like these, you can consider following the steps suggested below.
1. Guessing: Make an instinctive (quick) guess of what the answer could be, without any calculations.
2. Calculating using estimation and approximation —
(i) Describe the relationships among the quantities that are needed to find the answer.
(ii) Make reasonable assumptions and approximations if the required information is not available.
(iii) Compute and find the answer (and check how close your guess was).
Would the number of coins be in hundreds, thousands, lakhs, crores, or even more? Make an instinctive guess.
Solution:
1. Guessing: The number of coins might be in thousands.

2. Estimation and Approximation:
(i) Number of coins = Roxie’s weight ÷ Weight of one coin.

(ii) Assuming Roxie’s weight = 45 kg = 45,000 grams and each 1-rupee coin weighs 5 grams.
(iii) Number of coins = 45,000 ÷ 5 = 9,000 coins.
Thus, Roxie would need around 9,000 one-rupee coins to match her weight.
Conclusion: Our guess was in the right range — thousands.

Q. Estu says, “When I become an adult, I would like to donate notebooks worth my weight every year”. Roxie says, “When I grow up, I would like to do annadāna (offering grains or meals) worth my weight every year”.
How many people might benefit from each of these offerings in a year? Again, guess first before finding out.
Solution:
Estu’s notebook donation:
1. Guessing: Maybe around 70 – 80 children could benefit.

2. Calculating using estimation and approximation —
(i) Number of possible beneficiaries = Estu’s weight ÷ Weight of each notebook.
(ii) Assuming Estu’s weight = 50 kg = 50,000 grams, and each notebook weighs about 300 grams
(iii) Beneficiaries = 50,000 ÷ 300 = 166.67 ≈ 167.
Thus, approximately 167 children might benefit from the notebooks Estu would donate every year.

Roxie’s annadāna:
1. Guessing: Maybe around 100 people could benefit.

2. Calculating using estimation and approximation —
(i) Number of possible beneficiaries = Roxie’s weight ÷ Weight of grains/meal given to one person.
(ii) Assuming Roxie’s weight = 45 kg = 45,000 grams, and the average grains/meal given per person = 500 grams
(iii) Beneficiaries = 45,000 ÷ 500 = 90.
Thus, about 90 people might benefit from the annadāna Roxie wishes to do in the future.

Q. Roxie and Estu overheard someone saying—“We did pādayātra for about 400 km to reach this place! We arrived early this morning.”
How long ago would they have started their journey?
Find answers by making necessary assumptions and approximations. Do guess first before calculating to check how close your guess was!
Solution:
1. Guessing: They might have started their journey 10 – 15 days ago.

2. Calculating using estimation and approximation:
(i) Days taken = Total distance ÷ Average distance walked per day.
(ii) Assuming an average person walks about 20 km/day.
(iii) Number of days = 400 ÷ 20 = 20 days.
They likely started around 20 days ago.
Our guess of 10–15 days was a bit low, but still in a reasonable range depending on walking speed.

Textbook Page 35

Q. How many times can a person circumnavigate (go around the world) the Earth in their lifetime if they walk non-stop? Consider the distance around the Earth as 40,000 km.
Solution:
Distance around the Earth = 40,000 km
Average walking speed ≈ 5 km/hr
Lifespan ≈ 80 years
Total walking time in a lifetime = 24h/day × 365 days/year × 80 years = 700,800 hours.
Total distance walked in a lifetime = 5 km/hr × 700,800 hours = 3,504,000 km.
Number of circumnavigations = 3,504,000 km ÷ 40,000 km = 87.6 times.
Thus, a person walking non-stop for 80 years at a steady pace of 5 km/h could circumnavigate the Earth about 88 times.

Linear Growth vs. Exponential Growth

Roxie tells Estu about a science-fiction novel she is reading where they build a ladder to reach
the moon, “… I wonder if we actually had a ladder like that, how many steps would it have?”.

Q. What do you think? Make an instinctive guess first.
Would the number of steps be in thousands, lakhs, crores, or even more?

Solution:
I think the number of steps in the ladder would be in crores.

Textbook Page 36

Q. Some examples of exponential growth we have seen earlier in this chapter are ‘The Stones that Shine’, ‘Magical Pond’, ‘How Many Combinations’. We shall explore more such interesting examples in a later chapter and also in the next grade.
Can you come up with some examples of linear growth and of exponential growth?
Solution:
Linear growth: In linear growth, the quantity increases by the same amount in each step.
1. Stacking Bricks: Adding one brick to a tower every minute: 1, 2, 3, 4… bricks → grows by 1 each minute.
2. Saving Pocket Money: If you save ₹10 every day, the total savings grow like: ₹10, ₹20, ₹30, ₹40… → increasing by ₹10 each day.
3. Walking Distance: If you walk 2 km every day, your total distance is: 2 km, 4 km, 6 km, 8 km… → increasing by 2 km per day.

Exponential Growth: In exponential growth, the quantity doubles (or multiplies) at each step.
1. Magical Coin: A coin that doubles every day: ₹1, ₹2, ₹4, ₹8, ₹16… → doubling each day.
2. Bacteria Growth: If one bacterium splits into two every hour: 1, 2, 4, 8, 16… bacteria → population doubles every hour.
3. Sharing a Video on Social Media: One person shares with 2, each of them with 2 more:
1, 2, 4, 8, 16, 32… Soon it can go viral!

Textbook Page 38 – 39

Q. Calculate and write the answer using scientific notation:
(i) How many ants are there for every human in the world?
(ii) If a flock of starlings contains 10,000 birds, how many flocks could there be in the world?
(iii) If each tree had about 10⁴ leaves, find the total number of leaves on all the trees in the world.
(iv) If you stacked sheets of paper on top of each other, how many would you need to reach the Moon?
Solution:
(i) Human population ≈ 8 × 10⁹ (8 billion)
Number of ants on Earth ≈ 2 × 10¹⁶
Numer of ants per human = 2 × 10¹⁶ ÷ 8 × 10⁹ = 0.25 × 10⁷ = 2.5 × 10⁶
So, there are about 2.5 × 10⁶ (2.5 million) ants for every human in the world.

(ii) Number of starlings in the world ≈ 1 × 10⁹ (1 billion)
Number of starlings in a flock = 10,000 = 1 × 10⁴
Number of flocks = 1 × 10⁹ ÷ 1 × 10⁴ = 1 × 10⁵
So, there are 1 × 10⁵ (1 lakh) starling flocks in the world.

(iii) Number of trees in the world ≈ 3 × 10¹²
Number of leaves on a tree = 10⁴ = 1 × 10⁴
Total number of trees on all the trees in the world = (3 × 10¹²) × (1 × 10⁴) = 3 × 10¹⁶
So, there are about 3 × 10¹⁶ leaves on all trees in the world.

(iv) Thickness of a sheet of paper ≈ 0.1 mm = 1 × 10⁻⁴ m
Distance to the Moon ≈ 3.84 × 10⁵ km = 3.84 × 10⁸ m
Number of sheets = 3.84 × 10⁸ ÷ 1 × 10⁻⁴ = ​3.84 × 10¹²
So, approximately 3.84 × 10¹² sheets are needed to reach the Moon.

Q. “How old are you?” asked Estu. “I completed 13 years a few weeks ago!” said Roxie.
“How old are you?” asked Estu again. “I’m 4840 days old today!” said Roxie.
“How old are you?” asked Estu again. “I’m ______ hours old!” said Roxie.
Make an estimate before finding this number. Estu: “I am 4070 days old today. Can you find out my date of birth?”
Solution:
(i) For Roxie:
Estimation: Roxie is around 5000 days × 24 hrs/day = 1,20,000 or 1.2 × 10⁵ hours old.
Exact Calculation: 4840 days × 24 hrs/day = 1,16,160 hours = 1.1616 × 10⁵ hours old

(ii) For Estu:
Estu says, “I am 4070 days old today.”
Today’s date: 28 July 2025
Converting 4070 days to years: 4070 ÷ 365 ≈ 11.15 years or about 11 years and 55 days.
So, Estu was born about 11 years and 55 days ago.
Starting from 28 July 2025, go back:
11 years → 28 July 2014
55 more days back → Around 3 June 2014.
Thus, Estu’s Date of Birth is 3 June 2014.

Q. If you have lived for a million seconds, how old would you be?
Solution:
1 million seconds = 10,00,000 seconds
1,000,000 ÷ 60 = 16,666.67 minutes
16,666.67 ÷ 60 ≈ 277.78 hours
277.78 ÷ 24 ≈ 11.57 days
So, If you have lived for a million seconds, you’re about 11.6 days old.

Textbook Page 40

Q. 10⁵ seconds ≈ 1.16 days and 10⁶ seconds ≈ 11.57 days. Think of some events or phenomena whose time is of the order of (i) 10⁵ seconds and (ii) 10⁶ seconds. Write them in scientific notation.
Solution:
10⁵ seconds ≈ 1.16 days – Time spent on a long weekend trip: 2 days (1.72 × 10⁵ seconds).

10⁶ seconds ≈ 11.57 days – Time taken by the moon to complete half a lunar cycle from new moon to full moon: 14 days (1.2 × 10⁶ seconds).

Textbook Page 42

Q. Calculate and write the answer using scientific notation:
(i)  If one star is counted every second, how long would it take to count all the stars in the universe? Answer in terms of the number of seconds using scientific notation.
(ii)  If one could drink a glass of water (200 ml) every 10 seconds, how long would it take to finish the entire volume of water on Earth?
Solution:
(i) Estimated number of stars in the universe ≈ 1 × 10²⁴ stars
Counting rate = 1 star per second
Total time taken to count all the stars in the universe = (1 × 10²⁴) ÷ 1 = 1 × 10²⁴ seconds.

(ii) Total volume of water on Earth ≈ 1.4 × 10⁹ km³
1 km³ = 1 × 10¹⁵ ml
Total water = 1.4 × 10⁹ × 1 × 10¹⁵ = 1.4 × 10²⁴ ml
Drinking speed = 1 glass every 10 seconds = 200 ml per 10 sec
Time to drinl 1 ml = 10 seconds ÷ 200 ml = 0.05 ml/sec
Time to drink all water = 1.4 × 10²⁴ ml × 0.05 sec/ml = 0.07 × 1024 = 0.07 × 10²⁴ = 7 × 10²²​ seconds.
Thus, it would take 7 × 10²² seconds to drink all the water on Earth at the rate of one glass every 10 seconds.

Textbook Page 43

Q. Continuing this, a thousand trillion is a quadrillion (1015). This pattern continues. Observe the names million (106), billion (109), trillion (1012), quadrillion (1015), quintillion (1018), sextillion (1021), septillion (1024), octillion (1027), nonillion (1030), decillion (1033).
What does the first part of each name denote?
Solution:

Textbook Page 44 – 45

Figure it Out

1. Find out the units digit in the value of 2²²⁴ ÷ 4³² ?
Solution:
2²²⁴ ÷ 4³²
= 2²²⁴ ÷ (2²)³²
= 2²²⁴ ÷ 2^2×32
= 2²²⁴ ÷ 2⁶⁴
= 2^{224 – 64} = 2¹⁶⁰

2¹ = 2 (units digit 2)
2² = 4 (units digit 4)
2³ = 8 (units digit 8)
2⁴ = 16 (units digit 6)
2⁵ = 32 (units digit 2)
2⁶ = 64 (units digit 4)
………..
………..
The pattern repeats after every 4 steps.
So, the unit’s digit of 2¹⁶⁰ is the same as that of 2⁴, which is 6.
Thus, the unit digit of 2²²⁴ ÷ 4³² is 6.

2. There are 5 bottles in a container. Every day, a new container is brought in. How many bottles would be there after 40 days?
Solution:
Number of bottles in a container = 5
Number of containers added every day = 1
Number of containers after 40 days = 40 containers
Total bottles in 40 containers = 5 × 40 = 200 bottles
Therefore, there would be 200 bottles after 40 days.

3. Write the given number as the product of two or more powers in three different ways. The powers can be any integers.
(i) 64³
(ii) 192⁸
(iii) 32^-5
Solution:
(i) 64³
64 = 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
64³ = (2⁶)³ = 2¹⁸
Three different ways:
1. 64³ = 2¹⁸ = 2⁹ × 2⁹
2. 64³ = 2¹⁸ = 2¹⁰ × 2⁸
3. 64³ = 2¹⁸ = 2⁶ × 2⁶ × 2⁶

(ii) 192⁸
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁶ × 3
192⁸ = (2⁶ × 3)⁸ = 2^{6 × 8} × 3⁸ = 2⁴⁸ × 3⁸
Three different ways:
1. 192⁸ = 2⁴⁸ × 3⁸ = 2⁴⁰ × 2⁸ × 3⁸ = 2⁴⁰ × (2×3)⁸ = 2⁴⁰ × 6⁸
2. 192⁸ = 2⁴⁸ × 3⁸ = (2²⁴×3⁴)×(2²⁴×3⁴)
3. 192⁸ = 2⁴⁸ × 3⁸ = (2⁶)⁸ × 3⁸

(iii) 32^-5
32 = 2 × 2 × 2 × 2 × 2 = 2⁵
32^-5 = (2⁵)^-5 = 2^-25
Three different ways:
1. 32^-5 = 2^-25 = 2^-15 × 2^-10
2. 32^-5 = 2^-25 = 2⁻⁵ × 2⁻⁵ × 2⁻⁵ × 2⁻⁵ × 2⁻⁵
3. 32^-5 = 2^-25 = 2^-5 × 2^-20

4. Examine each statement below and find out if it is ‘Always True’, ‘Only Sometimes True’, or ‘Never True’. Explain your reasoning.
(i)  Cube numbers are also square numbers.
(ii)  Fourth powers are also square numbers.
(iii)  The fifth power of a number is divisible by the cube of that number.
(iv)  The product of two cube numbers is a cube number.
(v)  q46 is both a 4th power and a 6th power (q is a prime number).
Solution:
(i) Only sometimes true.
Explanation: 64 = 2⁶ = (2³)² = (2²)³ is both a cube and a square.
But 8 = 2³ is a cube, not a square.

(ii) Always true.
Eplanation: 81= 3⁴ = (3²)² = 9².

(iii) Always true.
Explanation: a⁵ = a³⋅ a² and is divisible by a³.

(iv) Always true.
Expalanation: 8 ⋅ 27 = 2³⋅3³ = 6³ = 216.

(v) Never true.
Explanation:

5. Simplify and write these in the exponential form.
(i) 10^–2 × 10^–5
(ii) 5⁷ ÷ 5⁴
(iii) 9^–7 ÷ 9⁴
(iv) (13^–2)^–3
(v) m⁵n¹²(mn)⁹
Solution:
(i) 10^–2 × 10^–5 = 10^{-2 – 5} = 10^-7

(ii) 5⁷ ÷ 5⁴ = 5^{7 – 4} = 5³

(iii) 9^–7 ÷ 9⁴ = 9^{-7 + 4} = 9^–3

(iv) (13^–2)^–3 = 13^{-2 × -3} = 13⁶

(v) m⁵n¹²(mn)⁹ = m⁵n¹²⋅m⁹n⁹ = m⁵⁺⁹n¹²⁺⁹ = m¹⁴n²¹

6. If 12² = 144 what is
(i) (1.2)²
(ii) (0.12)²
(iii) (0.012)²
(iv) 120²
Solution:

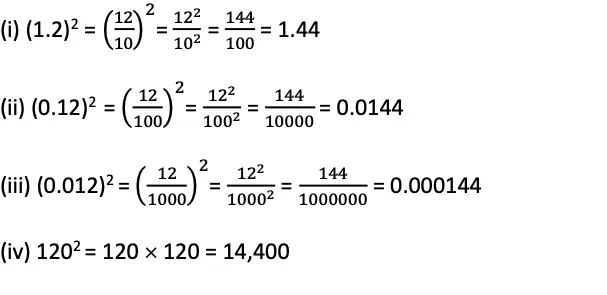
7. Circle the numbers that are the same —
2⁴ × 3⁶ , 6⁴ × 3² , 6¹⁰ , 18² × 6² , 6²⁴
Solution:
(i) 2⁴ × 3⁶

(ii) 6⁴ × 3² = (2 × 3)⁴ × 3² = 2³ × 3⁴ × 3² = 2³ × 3⁶

(iii) 6¹⁰ = (2 × 3)¹⁰ = 2¹⁰ × 3¹⁰

(iv) 18² × 6² = (2 × 3 × 3)² × (2 × 3)² = 2² × 3² × 3² × 2² × 3² = 2⁴ × 3⁶

(v) 6²⁴ = (2 × 3)²⁴ = 2²⁴ × 3²⁴

8. Identify the greater number in each of the following —
(i) 4³ or 3⁴ (ii) 2⁸ or 8² (iii) 100² or 2¹⁰⁰
Solution:
(i) 4³ or 3⁴
4³ = 64 , 3⁴ = 81
So, 3⁴ is greater.

(ii) 2⁸ or 8²
2⁸ = 256, 8² = 64
So, 2⁸ is greater.

(iii) 100² or 2¹⁰⁰
100² = 10,000
2¹⁰⁰ = (2¹⁰)¹⁰ = 1024¹⁰ which is a very large number, far greater than 10,000.
So, 2¹⁰⁰ is greater than 100².

9. A dairy plans to produce 8.5 billion packets of milk in a year. They want a unique ID (identifier) code for each packet. If they choose to use the digits 0–9, how many digits should the code consist of?
Solution:
8.5 billion=8,500,000,000

Therefore, the code should contain at least 10 digits to get a unique ID for each packet.

10. 64 is a square number (8²) and a cube number (4³). Are there other numbers that are both squares and cubes? Is there a way to describe such numbers in general?
Solution:
Yes, there are other numbers that are both squares and cubes. For example:
729 = 9³ (cube number) = 27² (perfect square)
4096 = 16³ (cube number) = 64² (perfect square)
General Rule: Any number that is a perfect sixth power (i.e., n⁶) is both a square and a cube. i.e.
1⁶ = 1
2⁶ = 64
3⁶ = 729
4⁶ = 4096
5⁶ = 15,625

11. A digital locker has an alphanumeric (it can have both digits and letters) passcode of length 5. Some example codes are G89P0, 38098, BRJKW, and 003AZ. How many such codes are possible?
Solution:
Length of passcode = 5
Total choices of alphabets and letters for each slot = 26 + 10 = 36
Total possible codes = 36 × 36 × 36 × 36 × 36 = 36⁵

12. The worldwide population of sheep (2024) is about 10⁹, and that of goats is also about the same. What is the total population of sheep and goats?
(i) 20⁹ (ii) 10¹¹ (iii) 10¹⁰
(iv) 10¹⁸ (v) 2 × 10⁹ (vi) 10⁹ + 10⁹
Solution:
Population of sheep = 10⁹
Population of goats = 10⁹
Total population of sheep and goats = 10⁹ + 10⁹
Therefore, (vi) 10⁹ + 10⁹ is the correct answer.

13. Calculate and write the answer in scientific notation:
(i)  If each person in the world had 30 pieces of clothing, find the total number of pieces of clothing.
(ii)  There are about 100 million bee colonies in the world. Find the number of honeybees if each colony has about 50,000 bees.
(iii)  The human body has about 38 trillion bacterial cells. Find the bacterial population residing in all humans in the world.
(iv) Total time spent eating in a lifetime in seconds.
Solution:
(i) Estimated world population: ≈ 8 billion = 8 × 10⁹
Number of pieces of clothing each person had = 30 pieces
Total number of pieces of clothing = 8×10⁹ × 30 = 2.4 × 10¹¹

(ii) Number of bees colonies in the world = 100 million = 1×10⁸
Number of bees in a colony = 50,000 = 5 × 10⁴
Total number of honeybees = 1 × 10⁸ × 5 × 10⁴ = 5 × 10¹²

(iii) World population ≈ 8 × 10⁹
Number of bacterial cells in human body = 38 trillion = 3.8 × 10¹³
Total bacterial population residing in all humans in the world = (3.8 × 10¹³)× (8 × 10⁹) = 30.4 × 10²² = 3.04 × 10²³

(iv) Average person’s lifespan = 80 years
Time spent eating daily ≈ 1.5 hours/day
1 hour = 3600 seconds
Total eating time per day = 1.5 × 3600 = 5400 seconds
Number of days in 80 years ≈ 80 × 365 = 29,200
Total seconds spent eating in a lifetime = 5400 × 29,200 = 1.5768 × 10⁸

14. What was the date 1 arab/1 billion seconds ago?
Solution:
1 billion seconds = 1,000,000,000 seconds
1,000,000,000 ÷ (60 × 60 × 24 × 365.25) ≈ 31.69 years
This means: 31 full years and 0.69 × 365.25 ≈ 252 days
Today is: 28 July 2025
Subtract 31 years → 28 July 1994
From 28 July 1994, go back 252 days, which lands around 18 November 1993.
So, ​​​1 nillion seconds ago was 18 November 1993.