Class 8 Maths Ganita Prakash Chapter 3 A Story of Numbers NCERT Solutions

Textbook Page 51 – 52

The Mechanism of Counting

Imagine that we are living in the Stone Age, say, around ten thousand years ago. Suppose we have a herd of cows. Here are some natural questions that we might ask about our herd —
Q1. How do we ensure that all cows have returned safely after grazing?
Q2. Do we have fewer cows than our neighbour?
Q3. If there are fewer, how many more cows would we need so that we have the same number of cows as our neighbour?
We need to tackle these questions without the use of the number names or written numbers of the Hindu number system. How do we do it?
Here are some possible methods.
Method 1: We could tackle the questions by using pebbles, sticks or any object that is available in abundance. Let us choose sticks. For every cow in the herd, we could keep a stick. The final collection of sticks tells us the number of cows, which can be used to check if any cows have gone missing.
This way of associating each cow with a stick, such that no two cows are associated or mapped to the same stick is called a one-to-one mapping. This mapping can then be used to come up with a way to represent numbers, as shown in the table.

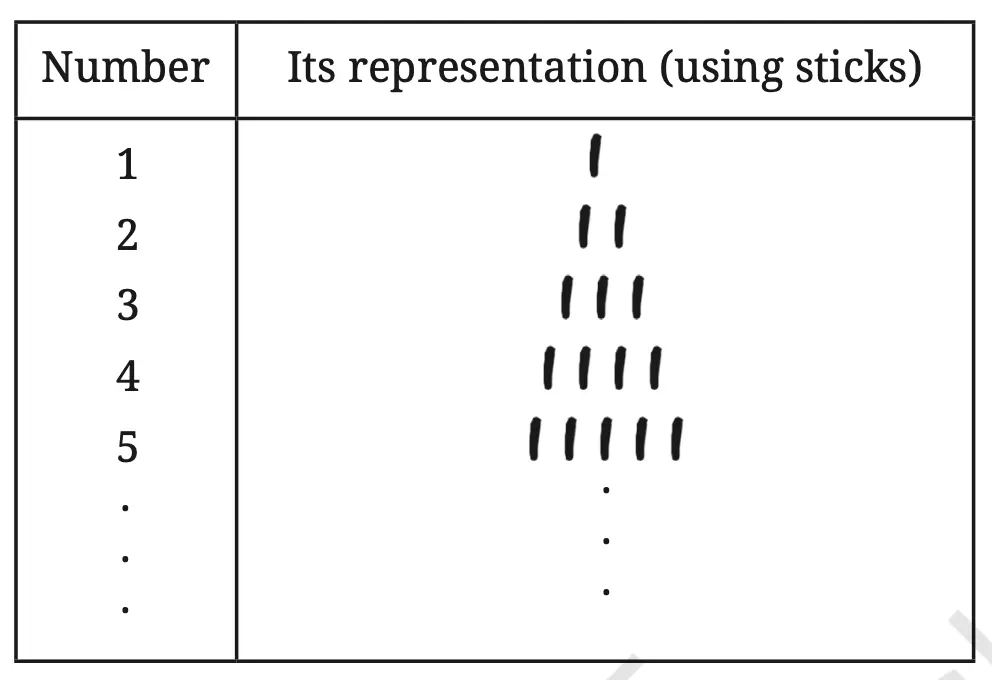
Q. How will you use such sticks to answer the other two questions (Q2 and Q3)?
Solution:
Q2. Do we have fewer cows than our neighbour?
Answer: (i) Represent your herd using one stick per cow and ask your neighbour to do the same.
(ii) Match your sticks one-to-one with your neighbour’s.
(iii) If both piles are exhausted at the same time, you both have equal cows.
If your pile finishes first but your neighbour still has some sticks, you have fewer cows.
If your neighbour’s pile finishes first, you have more cows.

Q3. If there are fewer, how many more cows would we need so that we have the same number of cows as our neighbour?
Answer: (i) Use the same one-to-one matching of sticks as in Q2.
(ii) Count extra sticks left in your neighbour’s pile after matching.
(iii) The number of extra sticks in their pile is the number of cows you are short by, and you need that many cows.

Method 2: Instead of objects, we could use a standard sequence of sounds or names. For example, we could use the sounds of the letters of any language. While counting, we could make a one-to-one mapping between the objects and the letters: that is, associate each object to be counted with a letter, following the letter-order. This mapping can then be used to come up with a way of verbally representing numbers.
For example, we get the following number representation if we use English letters ‘a’ to ‘z’.

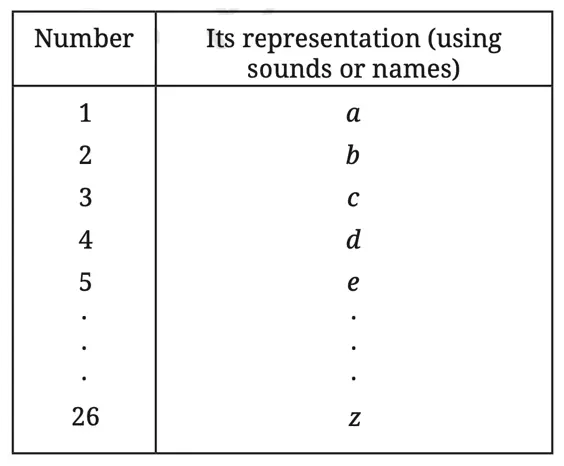
An obvious limitation of using only the letters of the English alphabet in this form is that it cannot be used to count collections having more than 26 objects.

Q. How many numbers can you represent in this way using the sounds of the letters of your language?
Solution:
We can represent 52 numbers in this way by using the sounds of the letters of the Hindi language.

Method 3: We could use a sequence of written symbols as follows.

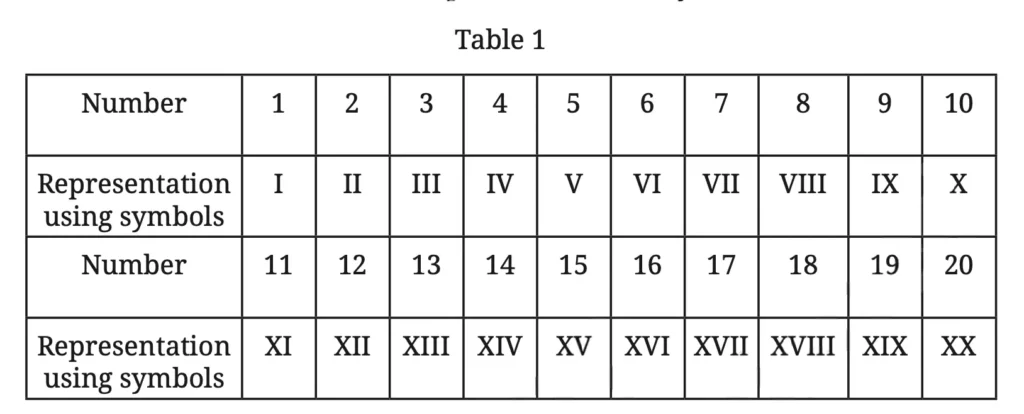
Q. Do you see a way of extending this method to represent bigger numbers as well? How?
Solution:
Yes, this method can be extended to represent much larger numbers by combining the basic symbols using the additive and subtractive rules. 
Rules to extend the system:
(i) Additive rule: If a smaller or equal symbol comes after a larger one, add the values.
Example: XV = 10 + 5 = 15
MCC = 1000 + 100 + 100 = 1200
(ii) Subtractive rule: If a smaller symbol comes before a larger one, subtract the smaller from the larger.
Example: IV = 5 − 1 = 4
IX = 10 − 1 = 9

Textbook Page 54

Figure it out

1. Suppose you are using the number system that uses sticks to represent numbers, as in Method 1. Without using either the number names or the numerals of the Hindu number system, give a method for adding, subtracting, multiplying and dividing two numbers or two collections of sticks.
Solution:
1. Addition: (i) Take two groups of sticks (say group A and B).
(ii) Put both groups together in a single pile.
(iii) The resulting pile shows the total quantity.

2. Subtraction: (i) Start with the group having more sticks.
(ii) Remove from it the number of sticks in the smaller group by physically taking that many sticks away.
(iii) The remaining sticks in the pile show the difference.

3. Multiplication: (i) Take one group of sticks (say, representing one set).
(ii) Repeat this group the number of times as indicated by the second group (e.g., 4 times).
(iii) Put all repeated groups together in one pile. The final collection shows the product.

4. Division: (i) Start with a pile of sticks (the total quantity).
(ii) Distribute the sticks one by one into equal-sized groups (e.g., for equal sharing).
(iii) The number of sticks in each group is the quotient, and any leftover sticks are the remainder.

2. One way of extending the number system in Method 2 is by using strings with more than one letter — for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!
Solution:
One of the ways of extending the number system in Method 2 by using strings with more than one letter is:

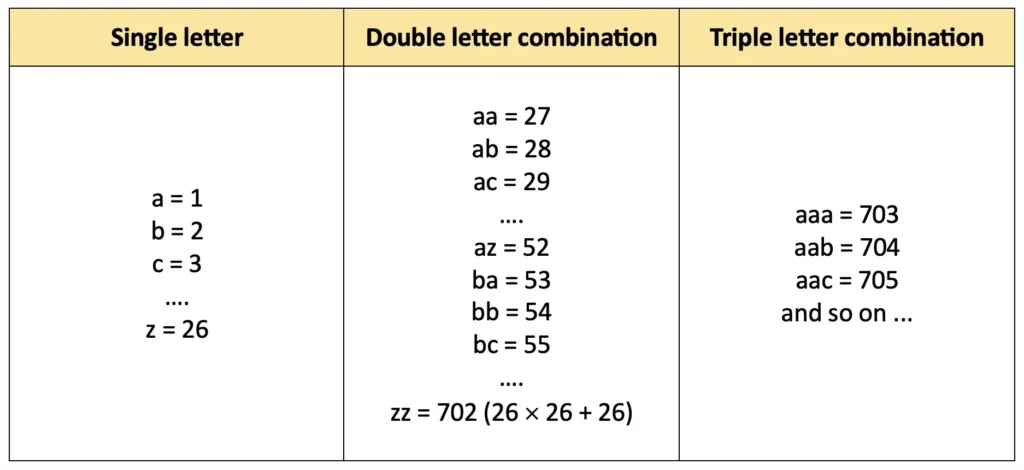
Textbook Page 58

Q. What could be the difficulties with using a number system that counts only in groups of a single particular size? How would you represent a number like 1345 in a system that counts only by 5s?
Solution:
The difficulties with using a number system that counts only in groups of a single particular size are:
(i) Numbers that are not multiples of 5 cannot be directly represented and need a way to handle the remainder after grouping in 5s.
(ii) Representing large numbers might need a large number of symbols or steps, which is time-consuming and inefficient.
(iii) Operations like addition, subtraction, or especially division and multiplication become more complex with fixed-size groupings.

1345 ÷ 5 = 269 remainder 2.
So:
1345 = 5 × 269
In a system that only counts in 5s, you would show:
269 groups of 5 with 0 leftover.

Textbook Page 59

Figure it Out

1. Represent the following numbers in the Roman system.
(i) 1222 (ii) 2999 (iii) 302 (iv) 715
Solution:
(i) 1222 = 1000 + 100 + 100 + 10 + 10 + 1 + 1 = MCCXXII.
(ii) 2999 = 1000 + 1000 + 900 + 90 + 9 = 1000 + 1000 + (1000 – 100) + (100 – 10) + (10 – 1) = MMCMXCIX.
(iii) 302 = 100 + 100 + 100 + 1 + 1 = CCCII.
(iv) 715 = 500 + 100 + 100 + 10 + 5 = DCCXV.

Example: Try adding the following numbers without converting them to Hindu numerals:
(a) CCXXXII + CCCCXIII
Let us find the total number of Is, Xs, and Cs, and group them starting from the largest landmark number.
Apparently, it looks like the largest landmark number is C, but note that 5 Cs (100s) make a D (500). So the sum is

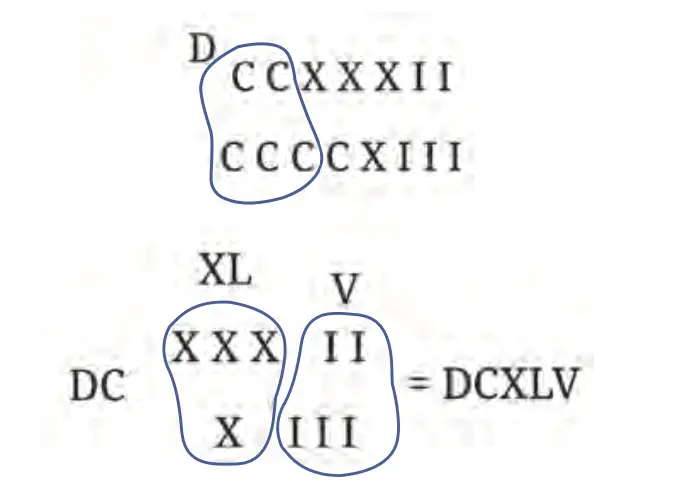
Q. Do it yourself now:
(b) LXXXVII + LXXVIII
Solution:

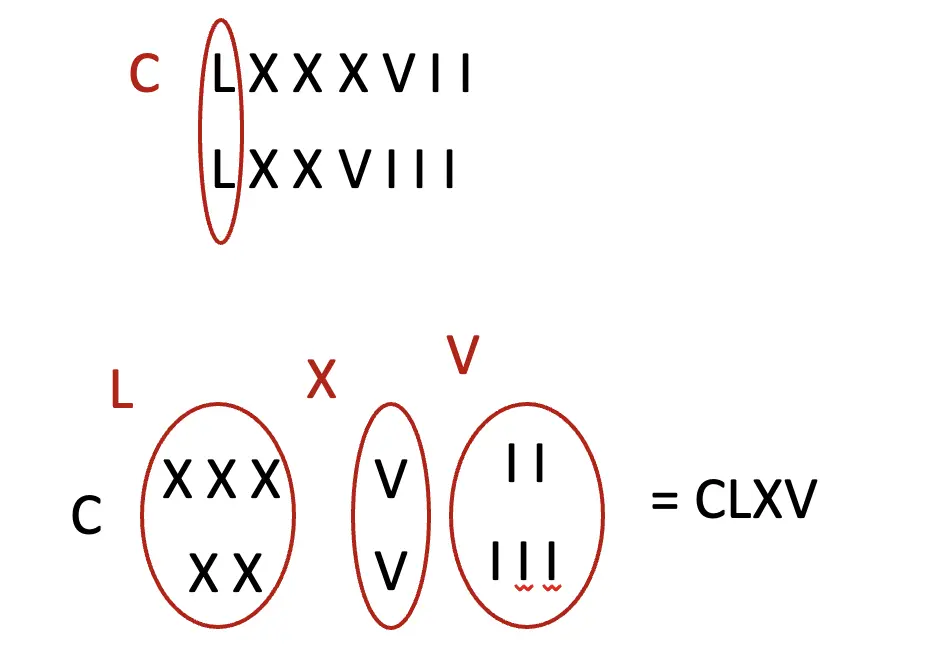
Textbook Page 60 – 61

Q. How will you multiply two numbers given in Roman numerals, without converting them to Hindu numerals? Try to find the product of the following pairs of landmark numbers: V × L, L × D, V × D, VII × IX.
Solution:
Multiplying two numbers given in Roman numerals without converting them to Hindu-Arabic numerals can be done using methods such as repeated addition or doubling and halving techniques.
For example, to compute V × L, we add V (five) a total of L (fifty) times.
(i) V × L = L + L + L + L + L = 50 + 50 + 50 + 50 + 50 = 100 + 100 + 50 = CCL.

(ii) L × D = D + D + D + ….. 50 times = 500 + 500 + 500 + ……. 50 times = 25,000

(iii) V × D = D + D + D + D + D = 500 + 500 + 500 + 500 + 500 = 1000 + 1000 + 500 = MMD.

(iv) VII × IX = VII + VII + VII + VII + VII + VII + VII + VII + VII = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 63 = 50 + 10 + 3 = LXIII.

Figure it Out

1. A group of indigenous people in a Pacific island use different sequences of number names to count different objects. Why do you think they do this?
Solution:
They use different number sequences because:
(i) Different objects (like coconuts, fish) may have different social, cultural, or economic importance. So, using different number names helps emphasize the context and value of what is being counted.
(ii) These counting systems are often passed down orally. Using object-specific counting sequences helps people remember quantities easily.
(iii) Not all cultures developed a general-purpose, abstract number system like Hindu-Arabic numerals. Instead, they built specific systems, like number names, to count different objects.

2. Consider the extension of the Gumulgal number system beyond 6 in the same way of counting by 2s. Come up with ways of performing the different arithmetic operations (+, –, ×, ÷) for numbers occurring in this system, without using Hindu numerals. Use this to evaluate the following:
(i)  (ukasar-ukasar-ukasar-ukasar-urapon) + (ukasar-ukasar- ukasar-urapon)
(ii)  (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasar- ukasar)
(iii)  (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
(iv)  (ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
Solution:
(i) (ukasar-ukasar-ukasar-ukasar-urapon) + (ukasar-ukasar- ukasar-urapon)
= (2 + 2 + 2 + 2 + 1) + (2 + 2 + 2 + 1)
= 9 + 7 = 16.

(ii) (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasar- ukasar)
= (2 + 2 + 2 + 2 + 1) – (2 + 2 + 2)
= 9 – 6 = 3.

(iii) (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
= (2 + 2 + 2 + 2 + 1) × (2 + 2)
= 9 × 4 = 36.

(iv) (ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
= (2 + 2 + 2 + 2 + 2 + 2 + 2 + 2) ÷ (2 + 2)
= 16 ÷ 4 = 4.

3. Identify the features of the Hindu number system that make it efficient when compared to the Roman number system.
Solution:
The Hindu number system is much more efficient than the Roman number system because:
(i) Large numbers are written compactly (e.g., 1,000,000), unlike Roman numerals, which become long and clumsy.
(ii) It uses place value, where a digit’s position (units, tens, hundreds) affects its value. Roman numerals lack this.
(iii) It includes zero, both as a number and a placeholder. Roman numerals have no symbol for zero.
(iv) It uses just 10 digits (0–9) to write any number, while Roman numerals need many symbols.
(v) Arithmetic operations are easy using standard rules. Roman operations are complex and often require conversion.

Textbook Page 62

1. Represent the following numbers in the Egyptian system: 10458, 1023, 2660, 784, 1111, 70707.
Solution:
(i) 10458 = 10000 + 100 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 =

(ii) 1023 = 1000 + 10 + 10 + 1 + 1 + 1 =

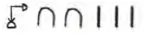
(iii) 2660 = 1000 + 1000 + 100 + 100 + 100 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 =

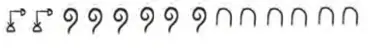
(iv) 784 = 100 + 100 + 100 + 100 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 =

(v) 1111 = 1000 + 100 + 10 + 1 =

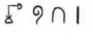
(vi) 70707 = 10000 + 10000 + 10000 + 10000 + 10000 + 10000 + 10000 + 100 + 100 + 100 + 100 + 100 + 100 + 100 + 1 + 1 + 1 + 1 + 1 + 1 + 1 =

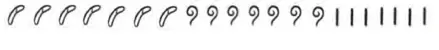
2. What numbers do these numerals stand for?

Solution:

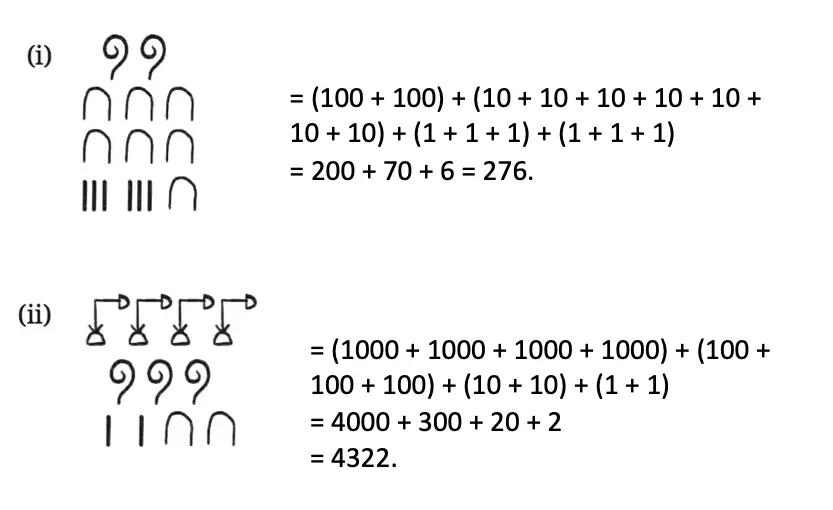
Textbook Page 63

Figure it Out

1. Write the following numbers in the above base-5 system using the symbols in Table 2: 15, 50, 137, 293, 651.
Solution:
(i) 15 = 5 + 5 + 5 =

(ii) 50 = 25 + 25 =

(iii) 137 = 125 + 5 + 5 + 1 + 1 =

(iv) 293 = 125 + 125 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 1 + 1 + 1 =

(v) 651 = 625 + 5 + 5 + 5 + 5 + 5 + 1 =

2. Is there a number that cannot be represented in our base-5 system above? Why or why not?
Solution:
There is no number that cannot be represented in base-5, because the system can express all whole numbers using combinations of digits 0 to 4 in increasing powers of 5.

3. Compute the landmark numbers of a base-7 system. In general, what are the landmark numbers of a base-n system?
Solution:
Starting with the first landmark number as 1, each landmark number of a base-7 system is 7 times the previous one. They are powers of 7 starting from 7⁰ = 1, 7¹ , 7² , 7³ , 7⁴ …..
The landmark numbers of a base-n number system are the powers of n starting from n⁰ = 1, n, n², n³,…

Textbook Page 65

Figure it Out

1. Add the following Egyptian numerals:

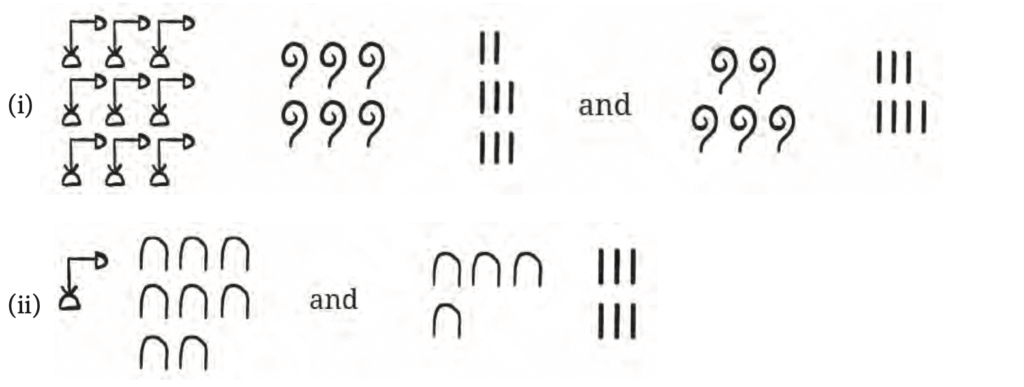
Solution:

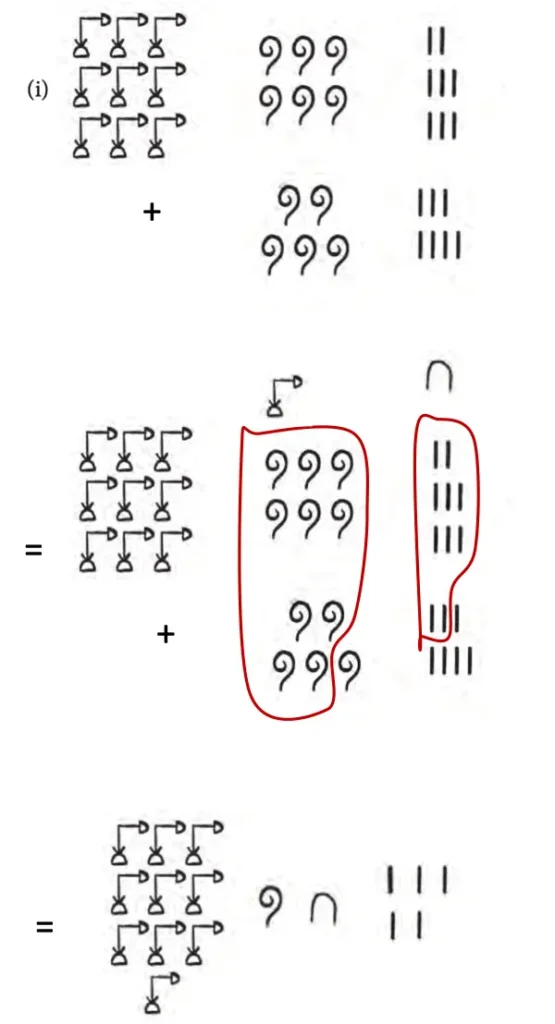
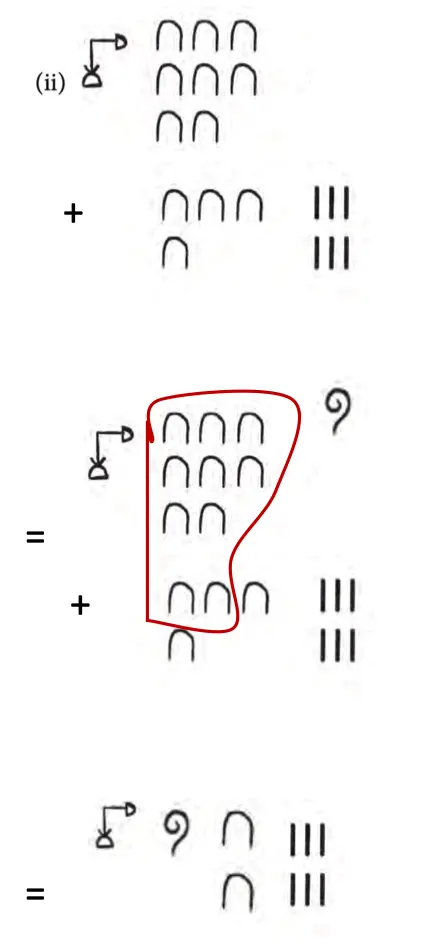
2. Add the following numerals that are in the base-5 system that we created:

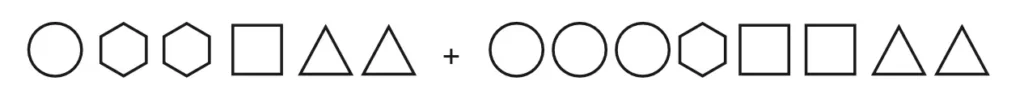
Solution: