Class 8 Maths Ganita Prakash Chapter 6 We Distribute, Yet Things Multiply NCERT Solutions

Textbook Page 142

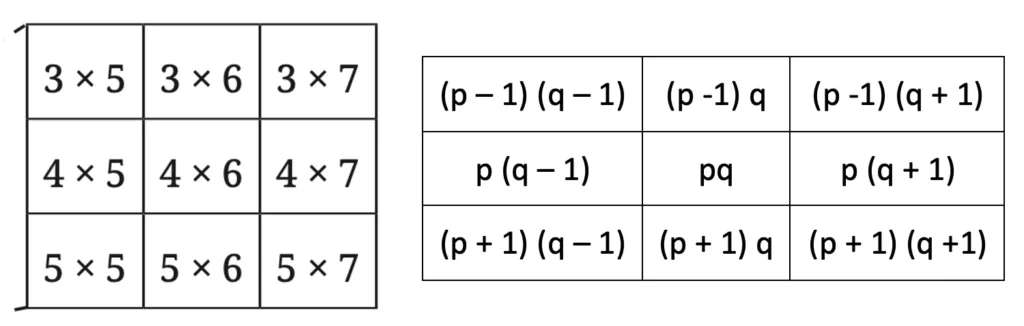
1. Observe the multiplication grid below. Each number inside the grid is formed by multiplying two numbers. If the middle number of a 3 × 3 frame is given by the expression pq, as shown in the figure, write the expressions for the other numbers in the grid.

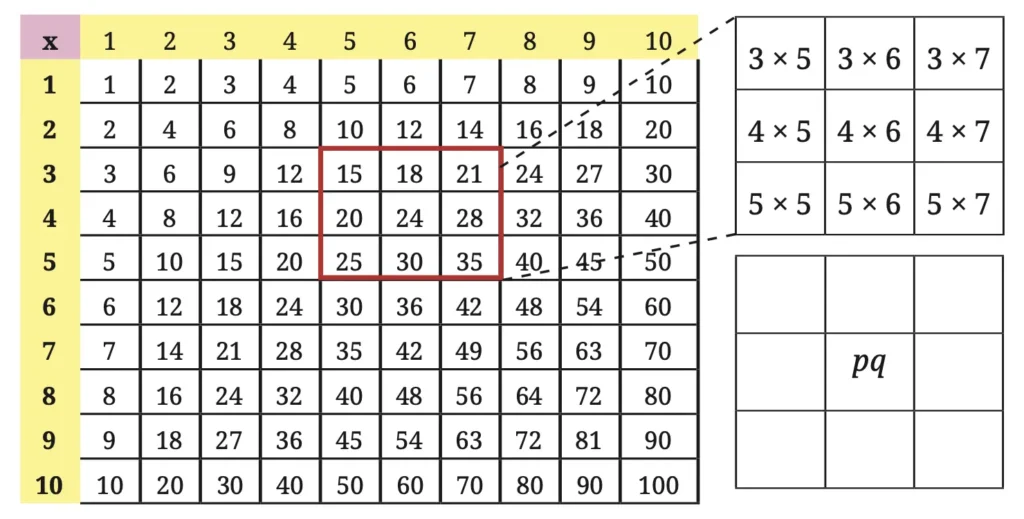
Solution:

2. Expand the following products.
(i) (3 + u) (v – 3)
(ii) 2/3 (15 + 6a)
(iii) (10a + b) (10c + d)
(iv) (3 – x) (x – 6)
(v) (–5a + b) (c + d)
(vi) (5 + z) (y + 9)
Solution:
(i) (3 + u) (v – 3)
= (3 + u)v – (3 + u)3
= 3 + uv – (9 + 3u)
= 3 + uv – 9 + 3u
= uv + 3u + 3 – 9
= uv + 3u – 6.

(iii) (10a + b) (10c + d)
= (10a + b)10c + (10 a + b)d
= 100ac + 10bc + 10ad + bd.

(iv) (3 – x) (x – 6)
= (3 – x)x – (3 – x)6
= 3x – x² – (18 – 6x)
= 3x – x² – 18 + 6x
= – x² + 6x + 3x – 18
= – x² + 9x – 18.

(v) (–5a + b) (c + d)
= (–5a + b)c + (–5a + b)d
= – 5ac + bc – 5ad + bd
= – 5ac – 5ad + bc + bd.

(vi) (5 + z) (y + 9)
= (5 + z)y + (5 + z)9
= 5y + zy + 45 + 9z
= 5y + 9z + zy + 45.

3. Find 3 examples where the product of two numbers remains unchanged when one of them is increased by 2 and the other is decreased by 4.
Solution:
If the two numbers are x and y, then:
x × y = (x + 2) × (y − 4)
xy = (x + 2)y – (x + 2)4
xy = xy + 2y – (4x + 8)
xy = xy + 2y – 4x – 8
xy – xy = 2y – 4x – 8
0 = 2y – 4x – 8
4x + 8 = 2y
2(2x + 4) = 2y
y = 2x + 4.
Examples:
(i) x = 1,  y = 6 → Product = 1 × 6 = 6
Check: (1 + 2) × (6 − 4) = 3 × 2 = 6.

(ii) x = 2, y = 8→ Product = 16
Check: (2 + 2) × (8 − 4) = 4 × 4 =16.

(iii) x = 5, y =14 → Product = 5 × 14 = 70
Check: (5 + 2) × (14 − 4) = 7 × 10 = 70.

Therefore, (1, 6), (2, 8), and (5, 14) are three valid examples.

4. Expand (i) (a + ab – 3b2) (4 + b), and (ii) (4y + 7) (y + 11z – 3).
Solution:
(i) (a + ab – 3b²) (4 + b)
= (a + ab – 3b²)4 + (a + ab – 3b²)b
= 4a + 4ab – 12b² + ab + ab² – 3b³
= – 3b³ – 12b² + ab² + 4ab + ab + 4a
= – 3b³ – 12b² + ab² + 5ab + 4a.

(ii) (4y + 7) (y + 11z – 3)
= (4y + 7)y + (4y + 7)11z – (4y + 7)3
= 4y² + 7y + 44yz + 77z – (12y + 21)
= 4y² + 7y + 44yz + 77z – 12y – 21
= 4y² + 7y – 12y + 44yz + 77z – 21
= 4y² – 5y + 44yz + 77z – 21.

5. Expand (i) (a – b) (a + b), (ii) (a – b) (a² + ab + b²), and (iii) (a – b)(a³ + a²b + ab² + b³), Do you see a pattern? What would be the next identity in the pattern that you see? Can you check it by expanding?
Solution:
(i) (a − b)(a + b)
= (a − b)a + (a − b)b
= a² – ab + ab – b²
= a² – b².

(ii) (a – b) (a² + ab + b²)
= (a – b)a² + (a – b)ab + (a – b)b²
= a³ – a²b + a²b – ab² + ab² – b³
= a³ – b³.

(iii) (a – b)(a³ + a²b + ab² + b³)
= (a – b)a³ + (a – b)a²b + (a – b)ab² + (a – b)b³
= a⁴ – a³b + a³b – a²b² + a²b² – ab³ + ab³ – b⁴
= a⁴ – b⁴.

The next identity would be: (a − b)(a⁴ + a³b + a²b² + ab³ + b⁴) = a⁵ − b⁵.