Class 8 Maths Ganita Prakash Chapter 7 Proportional Reasoning-1 NCERT Solutions

Textbook Page 165

Figure it Out

1. Circle the following statements of proportion that are true.
(i) 4 : 7 :: 12 : 21
(ii) 8 : 3 :: 24 : 6
(iii) 7 : 12 :: 12 : 7
(iv) 21 : 6 :: 35 : 10
(v) 12 : 18 :: 28 : 12
(vi) 24 : 8 :: 9 : 3
Solution:
(i) 4 : 7 :: 12 : 21
4 : 7 → Already in its simplest form.
12 : 21 → H.C.F = 3 → 12/3 : 21/3 = 4 :7.
Both ratios are equal, so the proportion is true.

(ii) 8 : 3 :: 24 : 6
8 : 3 → Already in its simplest form.
24 : 6 → H.C.F = 6 → 24/6 : 6/6 = 4 : 1.
Since both ratios are not equal, so the proportion is true.

(iii) 7 : 12 :: 12 : 7
7 : 12 → Already in its simplest form.
12 : 7 → Already in its simplest form.
Since both ratios are not equal, so the proportion is true.

(iv) 21 : 6 :: 35 : 10
21 : 6 → H.C.F = 3 → 21/3 : 6/3 = 7 : 2.
35 : 10 → H.C.F = 5 → 35/5 : 10/5 = 7 : 2.
Since both ratios are equal, so the proportion is true.

(v) 12 : 18 :: 28 : 12
12 : 18 → H.C.F = 6 → 12/6 : 18/6 = 2 : 3.
28 : 12 → H.C.F = 4 → 28/4 : 12/4 = 7 : 3.
Since both ratios are not equal, so the proportion is false.

(vi) 24 : 8 :: 9 : 3
24 : 8 → H.C.F = 8 → 24/8 : 8/8 = 3 : 1.
9 : 3 → H.C.F = 3 → 9/3 : 3/3 = 3 : 1.
Since both ratios are equal, so the proportion is true.

2. Give 3 ratios that are proportional to 4 : 9.
Solution:
To find ratios proportional to 4 : 9, we multiply both terms by the same number:
4 × 2 : 9 × 2 = 8 : 18.
4 × 3 : 9 × 3 = 12 : 27.
4 × 5 : 9 × 5 = 20 : 45.
So, three ratios proportional to 4 : 9 are 8 : 18; 12 : 27; and 20 : 45.

3. Fill in the missing numbers for these ratios that are proportional to 18 : 24.
3 : ______, 12 : ______, 20 : ______, 27 : ______
Solution:
Simplifying 18 : 24
H.C.F = 6 → 18/6 : 24/6 = 3 : 4.
So any proportional ratio must equal 3 : 4.
(i) 3 : ______ = 3 : 4
(ii) 12 : ______ = 3 × 4 : 4 × 4 = 12 : 16.
(iii) 20 : ______ = 3 × 20/3 : 4 × 20/3 = 20 : 80/3.
(iv) 27 : ______ = 3 × 9 : 4 × 9 = 27 : 36.

4. Look at the following rectangles. Which rectangles are similar to each other? You can verify this by measuring the width and height using a scale and comparing their ratios.

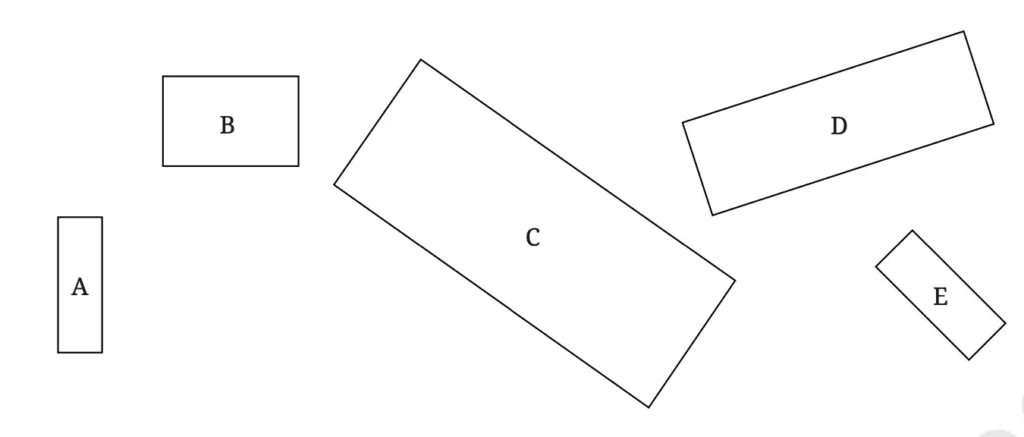
class 8 maths ganita prakash chapter 7 proportional reasoning-1 image 1

Solution:

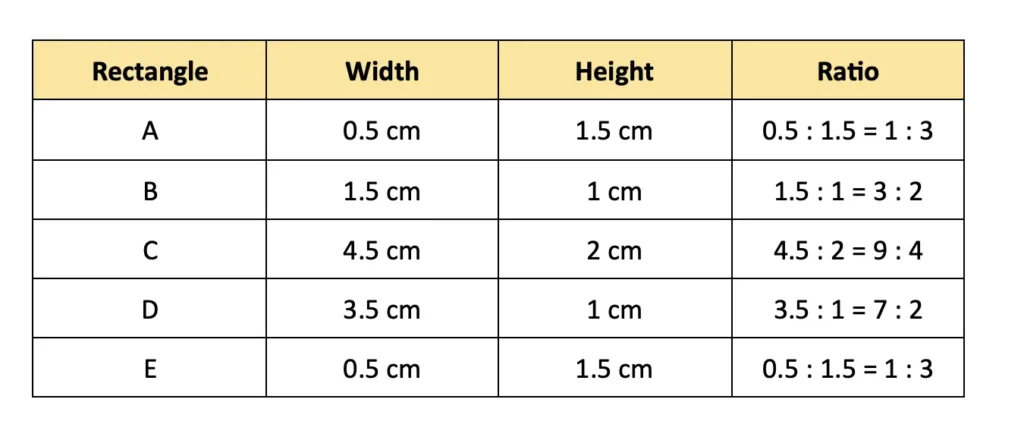
class 8 maths ganita prakash chapter 7 proportional reasoning-1 image 2

Since rectangles A and E have the same simplified ratio 1 : 3. So, they are similar to each other.

6. The following figure shows a small portion of a long brick wall with patterns made using coloured bricks. Each wall continues this pattern throughout the wall. What is the ratio of grey bricks to coloured bricks? Try to give the ratios in their simplest form.

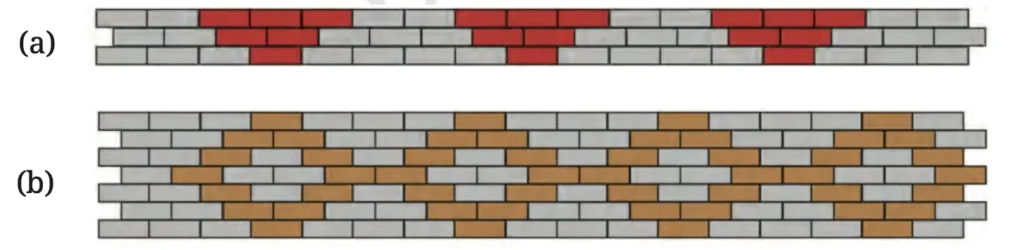
class 8 maths ganita prakash chapter 7 proportional reasoning-1 image 3

Solution:
(a) Grey bricks : Coloured bricks = 18 : 33 = 6 : 11.
(b) Gey bricks : Coloured bricks = 48 : 71.

7. Let us draw some human figures. Measure your friend’s body—the lengths of their head, torso, arms, and legs. Write the ratios as mentioned below—

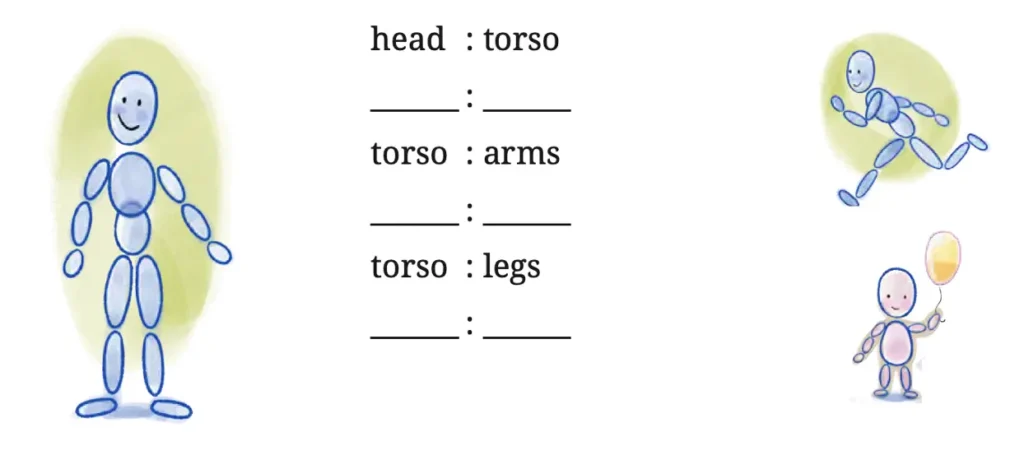
class 8 maths ganita prakash chapter 7 proportional reasoning-1 image 4

Solution:
My friend’s body measurements:
(i) Head = 22 cm
(ii) Torso (neck to hip) = 50 cm
(iii) Arms (shoulder to fingertip) = 60 cm
(iv) Legs (hip to foot) = 80 cm

1. Head : Torso = 22 : 50
Simplify by dividing both by 2 → 11 : 25.

2. Torso : Arms = 50 : 60
Simplify by dividing both by 10 → 5 : 6.

3. Torso : Legs = 50 : 80
Simplify by dividing both by 10 → 5 : 8.

So the ratios are:
• Head : Torso = 11 : 25
• Torso : Arms = 5 : 6
• Torso : Legs = 5 : 8

Similar Posts