Class 7 Maths Ganita Prakash Chapter 4 Expressions Using Letter-Numbers NCERT Solutions

Updated for the 2025-26 academic session, Class 7 Maths Ganita Prakash Chapter 4 Expressions Using Letter-Numbers NCERT Solutions are provided here. These solutions cover all the questions in Chapter 4, Expressions Using Letter-Numbers, and are intended to help the students prepare for the examinations of Class 7. The solutions provided here are written in self-explanatory and simple language, and students don’t need any external help to practice them. It is advised that the students must follow the chapter from the textbook, along with practicing these solutions to get their basics corrected.

Class 7 Maths Ganita Prakash Chapter 4 Expressions Using Letter-Numbers Questions Answers – PDF Download

Page 81

Q. Example 1: Shabnam is 3 years older than Aftab. When Aftab’s age 10 years, Shabnam’s age will be 13 years. Now Aftab’s age is 18 years, what will Shabnam’s age be? _______
Solution:
Shabnam is 3 years older than Aftab
Difference in Shabnam’s and Aftab’s age = 3 years
Aftab’s present age = 18 years
Shabnam’s present age = 18 + 3 = 21 years.

Page 82

Q. Use this expression to find Aftab’s age if Shabnam’s age is 20. (Expression: Aftab’s age = Shabnam’s age – 3.)
Solution:
If Shabnam’s age = 20 years
Then,
Aftab’s age = Shabnam’s age – 3
= 20 – 3
= 17 years.

Page 83

Q. Ketaki prepares and supplies coconut-jaggery laddus. The price of a coconut is ₹35 and the price of 1 kg jaggery is ₹60. How much should she pay if she buys 8 coconuts and 9 kg jaggery?
Solution:
Cost of 8 coconuts = 8 × 35 = ₹280
Cost of 9 kg jaggery = 9 × 60 = ₹540
Total money paid = ₹280 + ₹540 = ₹820.

Q. Use this expression (or formula) to find the total amount to be paid for 7 coconuts and 4 kg jaggery. (Expression: c × 35 + j × 60, where ‘c’ represents the number of coconuts and ‘j’ represents the number of kgs of jaggery)
Solution:
Number of coconuts (c) = 7
Number of kgs of jaggery (j) = 4kg
Total amount paid = c × 35 + j × 60
= 7 × 35 + 4 × 60
= 245 + 240
= ₹485.

Q. What is the perimeter of a square with side length 7 cm? Use the expression to find out. (Expression: 4 × q, where q stands for the side length.)
Solution:
Side length of square (q) = 7 cm
Perimeter = 4 × q
= 4 × 7
= 28 cm.

Page 84

Figure it Out

1. Write formulas for the perimeter of:
(a) triangle with all sides equal.
(b) a regular pentagon (as we have learnt last year, we use the word ‘regular’ to say that all side lengths and angle measures are equal)
(c) a regular hexagon
Solution:
(a) Triangle (3 equal sides): Perimeter = 3 × side length.

(b) Regular Pentagon (5 equal sides): Perimeter = 5 × side length.

(c) Regular hexagon (6 equal sides): Perimeter = 6 × side length.

2. Munirathna has a 20 m long pipe. However, he wants a longer watering pipe for his garden. He joins another pipe of some length to this one. Give the expression for the combined length of the pipe. Use the letter-number ‘k’ to denote the length in meters of the other pipe.
Solution:
Initial length of pipe = 20 m
Length of pipe joined = ‘k’ m
Expression: 20 + k.

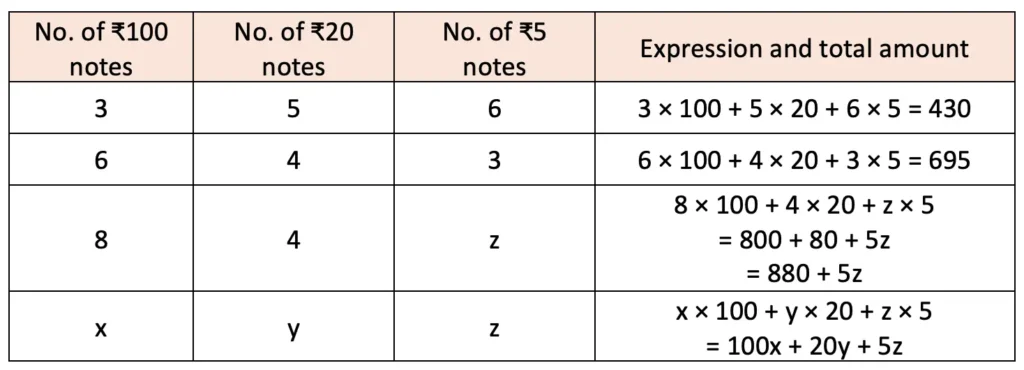
3. What is the total amount Krithika has, if she has the following numbers of notes of ₹100, ₹20 and ₹5? Complete the following table:

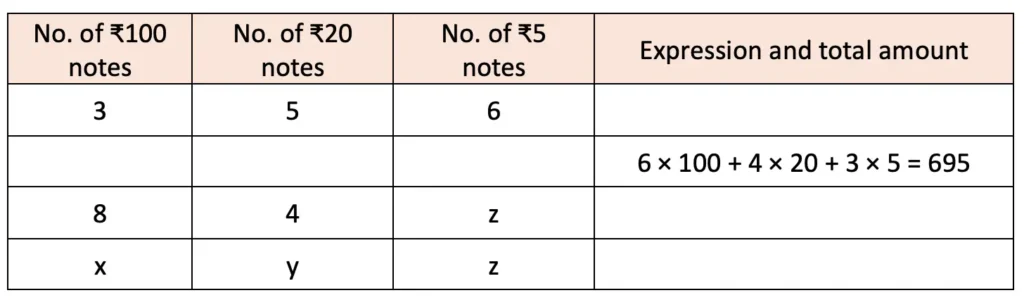
Solution:

4. Venkatalakshmi owns a flour mill. It takes 10 seconds for the roller mill to start running. Once it is running, each kg of grain takes 8 seconds to grind into powder. Which of the expressions below describes the time taken to complete grind ‘y’ kg of grain, assuming the machine is off initially?
(a) 10 + 8 + y      (b) (10 + 8) × y         (c) 10 × 8 × y      (d) 10 + 8 × y        (e) 10 × y + 8
Solution:
Time to start the machine = 10 seconds
Time to grind 1 kg of grain = 8 seconds
Quantity of grain = y kg
Total time = Time to start the machine + Time to grind y kg of grain
= 10 + 8 × y
Therefore, 10 + 8 × y is the correct answer.

5. Write algebraic expressions using letters of your choice.
(a) 5 more than a number
(b) 4 less than a number
(c) 2 less than 13 times a number
(d) 13 less than 2 times a number
Solution:
(a) x + 5 (Number = x)

(b) y – 4 (Number = y)

(c) 13 × p – 2 = 13p – 2 (Number = p)

(d) 2 × z – 13 = (Number = z)

Page 85

6. Describe situations corresponding to the following algebraic expressions:
(a) 8 × x + 3 × y
(b) 15 × j – 2 × k
Solution:
(a) Sum of 8 times x and 3 times y.

(b) Subtract 2 times k from 15 times j.

7. In a calendar month, if any 2 × 3 grid full of dates is chosen as shown in the picture, write expressions for the dates in the blank cells if the bottom middle cell has date ‘w’.

Solution:

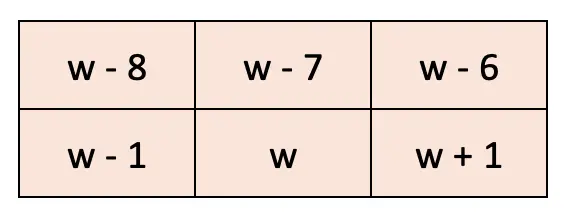
Q. Let us revise these concepts and find the values of the following expressions:
1. 23 – 10 × 2
2. 83 + 28 – 13 + 32
3. 34 – 14 + 20
4. 42 + 15 – (8 – 7)
5. 68 – (18 + 13)
6. 7 × 4 + 9 × 6
7. 20 + 8 × (16 – 6)
Solution:
1. 23 – 10 × 2 = 23 – 20 = 3.

2. 83 + 28 – 13 + 32 = 83 – 13 + 28 + 32 = 70 + 60 = 130.

3. 34 – 14 + 20 = 30 + 20 = 50.

4. 42 + 15 – (8 – 7) = 42 + 15 – 1 = 57 – 1 = 56.

5. 68 – (18 + 13) = 68 – 31 = 37.

6. 7 × 4 + 9 × 6 = 28 + 54 = 82.

7. 20 + 8 × (16 – 6) = 20 + 8 × 10 = 20 + 80 = 100.

Page 87

Q. 1. Observe each of them and identify if there is a mistake.
2. If you think there is a mistake, try to explain what might have gone wrong.
3. Then, correct it and give the value of the expression.
Solution:
1. Given equation: 10 – a = 6
Substitute a = -4
10 – (-4) = 6
10 + 4 = 6
14 ≠ 6
Since 14 ≠ 6, a = -4 does not satisfy the equation.
Now, 10 – a = 6
10 – 6 = a
a = 4.
Therefore, the solution to the equation is m = 16/3.

2. Given equation: 3d = 36
Substitute d = 6
3 × 6 = 36
18 ≠ 36
Since 18 ≠ 36, d = 6 does not satisfy the equation.
Now, 3d = 36
d = 36/3
d = 12.
Therefore, the solution to the equation is d = 12.

3. Given equation: 3s – 2 = 15
Substitute s = 7
3 × 7 – 2 = 15
21 – 2 = 15
19 ≠ 15
Since 19 ≠ 14, s = 7 does not satisfy the equation.
Now, 3s – 2 = 15
3s = 15 + 2
3s = 17
s = 17/3.
Therefore, the solution to the equation is s = 17/3.

4. Given equation: 2r + 1 = 29
Substitute r = 8
2 × 8 + 1 = 29
16 + 1 = 29
17 ≠ 29
Since 17 ≠ 29, r = 8 does not satisfy the equation.
Now, 2r + 1 = 29
2r = 29 – 1
2r = 28
r = 28/2 = 14.
Therefore, the solution to the equation is r = 14.

5. Given equation: 2j = 10
Substitute j = 5
2 × 5 = 10
10 = 10
Since 10 ≠ 10, j = 5 does satisfy the given equation.

6. Given equation: 3(m + 1)
Substitute m = -6,
3(-6 + 1) = 19
3(-5) = 19
-15 ≠ 19
Since -15 ≠ 19; m = -6 does not satisfy the equation.
3(m + 1) = 19
3m + 3 = 19
3m = 19 – 3
3m = 16
m = 16/3
Therefore, the solution to the equation is m = 16/3.

7. Given equation: 2f – 2g = 2
Substitute f =3, g = 1,
2 × 3 – 2 × 1 = 2
6 – 2 = 2
4 ≠ 2
Since 4 ≠ 2; f =3, g = 1 do not satisfy the equation.
If f = 2 and g = 1, then
2 × 2 – 2 × 1 = 2
4 – 2 = 2
2 = 2
Therefore, the solution to the equation are f = 2 and g = 1.

8. Given equation: 2t + b = 24
Substitute t = 4, b = 3,
2 × 4 + 3 = 24
8 + 3 = 24
11 ≠ 24
Since 11 ≠ 24, t = 4, b = 3 do not satisfy the equation.
Substitute t = 8, b = 8:
2 × 8 + 8 = 24
16 + 8 = 24
24 = 24
Therefore, the solution to the equation are t = 8, b = 8.

9. Given equation: h – (3 – n) = 4
Substitute h = 5, n = 6,
5 – (3 – 6) = 4
5 – (-3) = 4
5 + 3 = 4
8 ≠ 4
Since 11 ≠ 24, h = 5, n = 6 does not satisfy the equation.
Substitute h = 5, n = 2
5 – (3 – 2) = 4
5 – 1 = 4
4 = 4
Therefore, the solution to the equation are h = 5, n = 2.

Page 88

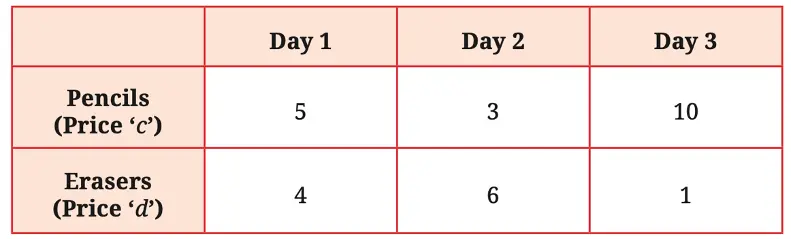
Q. If c = ₹50, find the total amount earned by the scale of pencils.
Solution:
Total amount earned = Day 1 + Day 2 + Day 3
= 5 × c + 3 × c + 10 × c
= 5c + 3c + 10c = 18c.
If c = ₹50, then
18c = 18 × 50 = ₹900.
Therefore, ₹900 is the total amount earned by the scale of pencils.

Q. Write the expression for the total money earned by selling erasers. Then, simplify the expression.
Solution:
Total amount earned = Day 1 + Day 2 + Day 3
= 4 × d + 6 × d + 1 × d
= 4d + 6d + d
= 11d.

Page 90

Q. A shop rents out chairs and tables for a day’s use. To rent them, one has to first pay the following amount per piece.
When the furniture is returned, the shopkeeper pays back some amount as follows.
Write an expression for the total number of rupees paid if x chairs and y tables are rented.
For x chairs and y tables, let us find the total amount paid at the beginning and the amount one gets back after returning the furniture.
Describe the procedure to get these amounts.

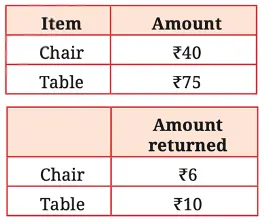
Solution:
Chairs rented = x
Tables rented = y
Total amount paid at the beginning = Amount paid for chairs + Amount paid for tables
= 40 × (x) + 75 × y
= 40x + 7y.
Total amount returned = Amount returned for chairs + Amount returned for tables
= 6 × (x) + 10 × y
= 6x + 10y.
Total amount paid = (40x + 75y) – (6x + 10y)

Q. Can we simplify this expression? If yes, how? If not, why not? [Expression: (40x + 75y) – (6x + 10y)]
Solution:
Yes, the expression can be simplified further as follows:
(40x + 75y) – (6x + 10y) = 40x + 75y – 6x – 10y
= (40x – 6x) + (75y – 10y)
= 34x + 65y.

Page 91

Q. Could we have written the initial expression as (40x + 75y) + (– 6x – 10y)?
Solution:
Yes, the initial expression (40x + 75y) – (6x + 10y) could also be written as
(40x + 75y) + (– 6x – 10y).
This is because subtracting a group of terms is the same as adding their negatives.

Q. What do each of the expressions mean? (Expressions: 7p – 3q, 8p – 4q, and 6p – 2q).
Solution:
Each of these expression involve a difference between two algebraic terms.

Page 92

Q. Give some possible scores for Krishita in the three rounds so that they add up to give 23p – 7q.
Solution:
Krishita’s score in three rounds could be (8p – 3q), (6p – 2q), and (9p – 2q).
Therefore, total score after three rounds = (8p – 3q) + (6p – 2q) + (9p – 2q).
= 8p – 3q + 6p – 2q + 9p – 2q
= 23p – 7q.

Q. Can we say who scored more? Can you explain why? (Charu’ score: 21p – 9q & Krishita’s score: 23p – 7q)
Solution:
Penalties for Charu = 9q
Penalities for Krishita = 7q
Krishita scored more because she had fewer penalties than Charu.

Q. Simplify this expression further. [Expression: (23p – 7q)– (21p – 9q)]
Solution:
23q – 7q – (21p – 9q) = 23q – 7q – 21p + 9q
= (23q – 21q) + (9q – 7q)
= 2q + 2q.

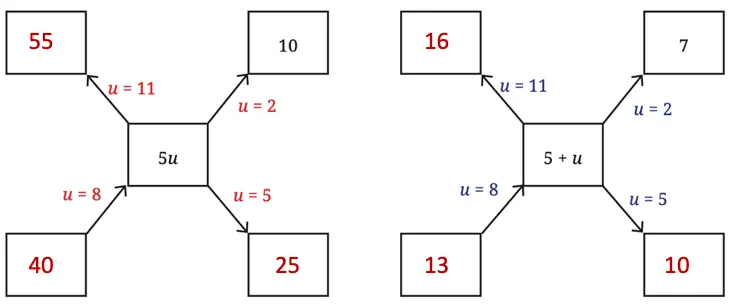
Q. Fill the blanks below by replacing the letter-numbers by numbers; an example is shown. Then compare the values that 5u and 5 + u take.

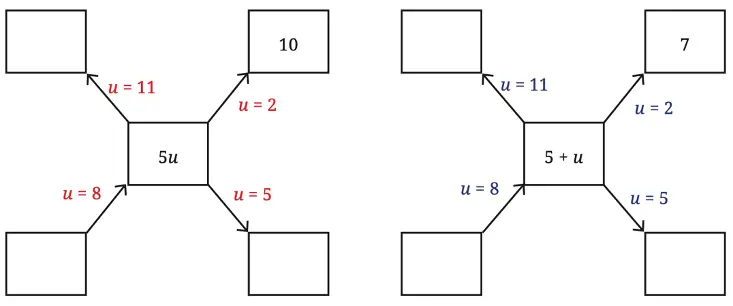
Solution:

Page 93

Q. Are the expressions 10y – 3 and 10(y – 3) equal? Let us compare the values that these expressions take for different values of y.

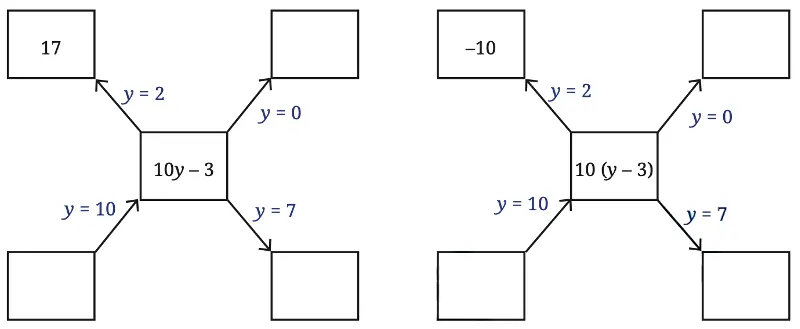
Solution:

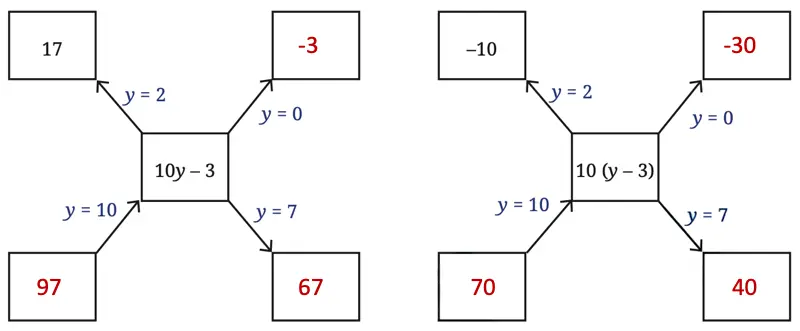
(i) For 10y – 3:
If y = 0, then 10y -3 = 10(0) – 3 = 0 – 3 = -3.
If y = 7, then 10y -3 = 10(7) – 3 = 70 – 3 = 67.
If y = 10, then 10y – 3 = 10(10) – 3 = 100 – 3 = 97.

(ii) For 10(y – 3):
If y = 0, then 10(y – 3) = 10(0 – 3) = 10(-3) = -30.
if y = 7, then 10(y – 3) = 10(7 – 3) = 10(4) = 40.
If y = 10, then 10(y – 3) = 10(10 – 3) = 10(7) = 70.

Q. After filling in the two diagrams, do you think the two expressions are equal?
Solution:
Filling in the two diagrams made it clear that the two expressions are not equal.

Page 94

Figure it Out

1. Add the numbers in each picture below. Write their corresponding expressions and simplify them. Try adding the numbers in each picture in a couple different ways and see that you get the same thing.

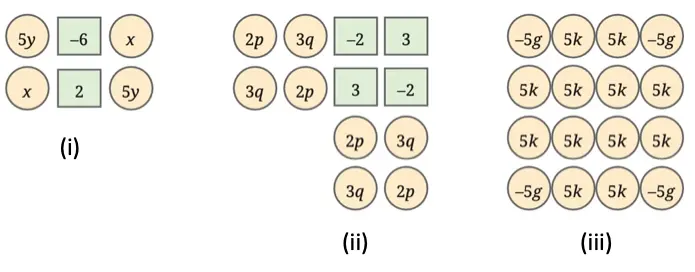
Solution:
(i) Adding like terms together gives:
(5y + 5y) + (x + x) + (2 – 6) = 10y + 2x + (-4) = 2x + 10y -4.

(ii) Adding like terms together gives:
(2p × 4) + (3q × 4) + (2 × -2) + (3 × 2) = 8p + 12q + (-4) + 6 = 8p + 12q + 2.

(iii) Adding like terms together gives:
(5k × 12) + (-5g × 4) = 60k + (-20g) = 40k – 20g.

2. Simplify each of the following expressions:
(a) p + p + p + p, p + p + p + q, p + q + p – q,
(b) p − q + p − q, p + q – p + q,
(c) p + q − (p + q), p – q – p – q,
(d) 2d – d – d – d, 2d – d – d – c,
(e) 2d – d − (d − c), 2d − (d − d) – c,
(f) 2d – d – c – c
Solution:
(a) p + p + p + p = 3p.
p + p + p + q = 3p + q.
p + q + p – q = 2q

(b) p − q + p – q = 2p -2q.
p + q – p + q = 2q.

(c) p + q − (p + q) = p + q – p – q = 0.
p – q – p – q = -2q.

(d) 2d – d – d – d = 2d – 3d = -d.
2d – d – d – c = 2d – 2d – c = -c.

(e) 2d – d − (d – c) = 2d – d – d + c = 2d – 2d + c = c.
2d − (d − d) – c = 2d – 0 – c = 2d – c.

(f) 2d – d – c – c = d – 2c.

Q. Some simplifications of algebraic expressions are done below. The expression on the right-hand side should be in its simplest form.
• Observe each of them and see if there is a mistake.
• If you think there is a mistake, try to explain what might have gone wrong.
• Then, simplify it correctly.

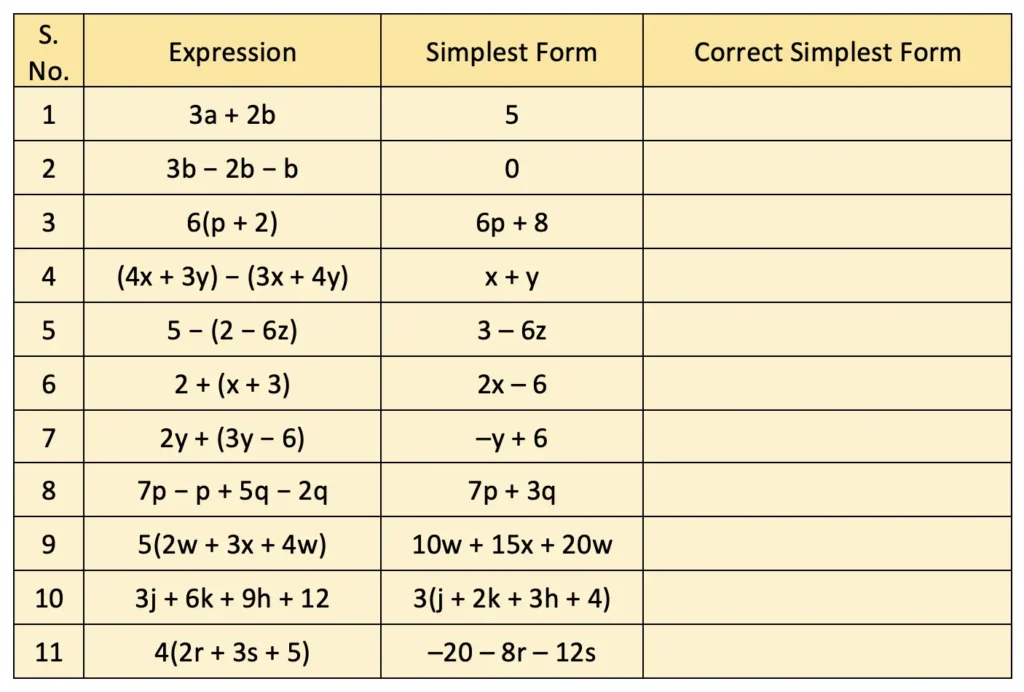
Solution:
1. Incorrect, simplest form because unlike terms 3a and 2b cannot be added.
Correct simplest form: 3a + 2b.

2. Correct simplest form because 3b – 2b – b = 3b – 3b = 0.

3. Incorrect simplest form because of wrong multiplication done during distribution.
Correct simplest form: 6(p + 2) = 6 × p + 6 × 2 = 6p + 12.

4. Incorrect, simplest form because of the subtraction mistake.
Correct simplest form: (4x + 3y) − (3x + 4y) = 4x + 3y – 3x – 4y
= 4x – 3x + 3y – 4y
= x – y.

5. Incorrect, simplest form because of the sign error.
Correct simplest form: 5 − (2 − 6z) = 5 – 2 + 6z = 3 + 6z.

6. Incorrect, simplest form because of the misapplied operations.
Correct simplest form: 2 + (x + 3) = 2 + x + 3 = x + 5.

7. Incorrect, simplest form because of incorrect combining.
Correct simplest form: 2y + (3y − 6) = 2y + 3y – 6 = 5y – 6.

8. Incorrect, simplest form because of addition and subtraction mistakes.
Correct simplest form: 7p − p + 5q − 2q = 6p + 3q.

9. Incorrect, simplest form because of incomplete simplification.
Correct simplest form: 5(2w + 3x + 4w) = 5 × 2w + 5 × 3x + 5 × 4w
= 10w + 15x + 20w
= 30w + 15x.

10. Correct simplest form.

11. Incorrect, simplest form because of multiplication done incorrectly and the signs are wrong.
Correct simplest form: 4(2r + 3s + 5) = (4 × 2r) + (4 × 3s) + (4 × 5)
= 8r + 12s + 20.

Q. Take a look at all the corrected simplest forms (i.e. brackets are removed, like terms are added, and terms with only numbers are also added). Is there any relation between the number of terms and the number of letter-numbers these expressions have?
Solution:
Combining like terms and simplifying constants reduces the total number of terms in an expression.

Page 96

Q.  Find the formulas of the number machines below and write the expression for each set of inputs.

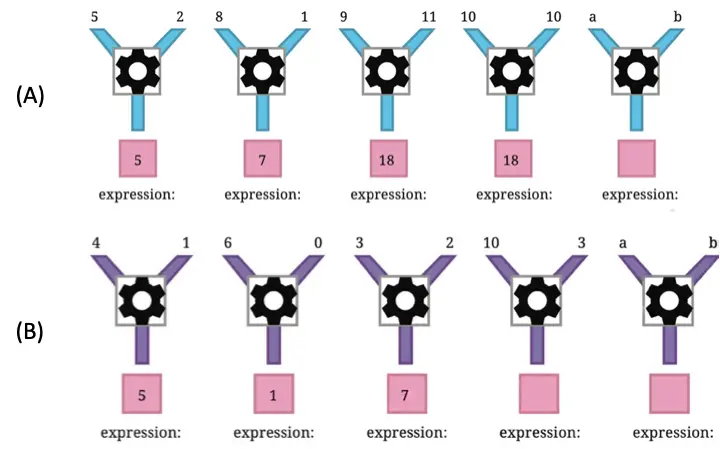
Solution:
(A) Formula: Two subtracted from the sum of the two numbers.
Algebraic expression: a + b – 2.
5th expression: a + b – 2.

(B) Formula: One added to the multiplication of two numbers.
Algebraic expression: (a × b) + 1 = ab + 1.
4th expression: 10 × 3 + 1 = 30 + 1 = 31.
5th expression: a × b + 1 = ab + 1.

Page 97

Q. Given a position number can we find out the design that appears there? Which Design appears at Position 122? (Position at which the design A, B and C appears for nth time are 3n-2, 3n-1 and 3n)
Solution:
Yes, given a position number can help us find out the design that appears there.
Since 122 ÷ 3 gives 40 as the quotient and a remainder of 2.
Therefore, Design B appears at Position 122.

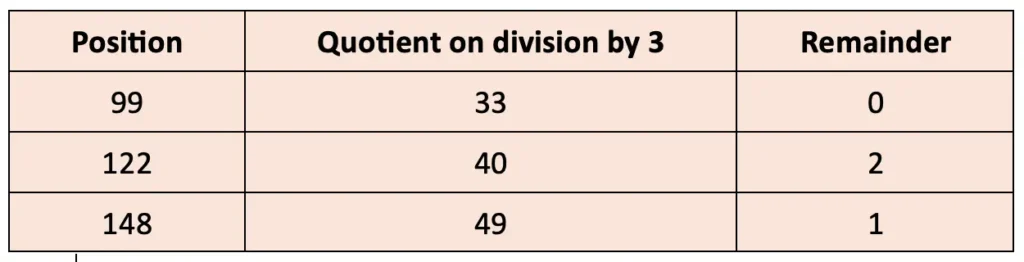
Q. Can the remainder obtained by dividing the position number by 3 be used for this? Observe the table below.

Solution:
Yes, the remainders can be used for this. When the position number is divided by 3: if the remainder is 0, the design at that position is Design C; if the remainder is 1, it’s Design A; and if the remainder is 2, it’s Design B.

Q. Use this to find what design appears at positions 99, 122, and 148.

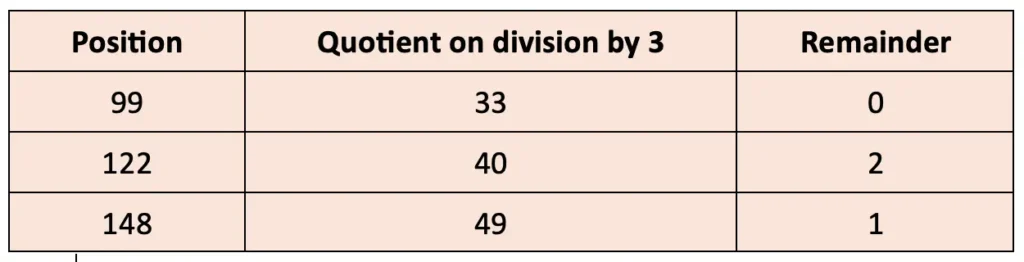
Solution:
Design C appears at position 99.
Design B appears at position 122.
Design A appears at position 148.

Page 99

Q. Verify this expression for diagonal sums by considering any 2 × 2 square and taking its top left number to be ‘a’.
Solution:
Considering the given 2 × 2 square:

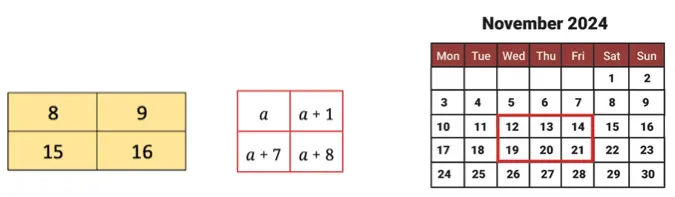
Top left number (8) = a
Number to the right 8 (9) = a + 1
Number below 8 (15) = a + 7
Number diagonal to 8 (16) = a + 8

First diagonal sum (8 + 16 = 24) = a + (a + 8) = 2a + 8.
Second diagonal sum (9 + 15 = 24) = (a + 1) + (a + 7) = 2a + 8.
Hence, verified that both diagonal sums are equal to 2a + 8.

Q. Find the sum of all the numbers. Compare it with the number in the centre: 15. Repeat this for another set of numbers that forms this shape. What do you observe?
Solution:

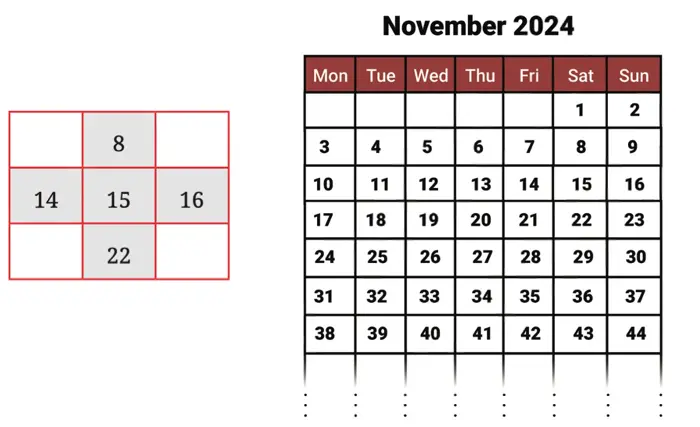
Sum of all numbers = 8 + 14 + 22 + 16 + 15 = 75.
Central number = 15.
75 is five times 15.

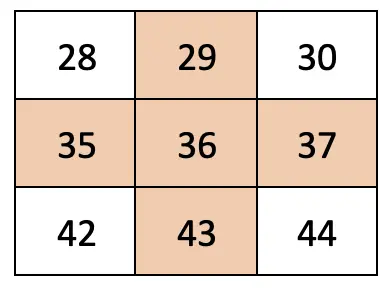
Repeating this for the above set of numbers:
Sum of all number = 29 + 35 + 43 + 37 + 36 = 180.
Central number = 36.
180 is five times 36.
Observation: The sum of a set of numbers forming a (+) shape is five times the central number of the shape.

Page 100

Q. How many matchsticks will there be in Step 33, Step 84, and Step 108? Of course, we can draw and count, but is there a quicker way to find the answers using the pattern present here?
Solution:
Matchsticks in Step 33 = (2 × 33) + 1 = 66 + 1 = 67.
Matchsticks in Step 84 = (2 × 84) + 1 = 168 + 1 = 169.
Matchsticks in Step 108 = (2 × 108) + 1 = 216 + 1 = 217.

Q. Does the above expression also give the number of matchsticks at each step correctly? Are these expressions the same? [Expression: 3 + 2 × (y – 1) and 2y + 1]
Solution:
Yes, both the expressions 3 + 2 × (y – 1) and 2y + 1 give the number of matchsticks at each step correctly. It is because both are exactly the same.
i.e., 3 + 2 × (y – 1) = 3 + 2y – 2 = 2y + 1.

Q. What are these numbers in Step 3 and Step 4?
Solution:
In Step 3, there are 3 matchsticks placed horizontally and 4 matchsticks placed diagonally.
In step 4, there are 4 matchsticks placed horizontally and 5 matchsticks placed diagonally.

Q. How does the number of matchsticks change in each orientation as the steps increase? Write an expression for the number of matchsticks at Step ‘y’ in each orientation. Do the two expressions add up to 2y + 1?
Solution:
Number of horizontal matchsticks per step = y
Number of diagonally placed matchsticks per step = y + 1

Total matchsticks for step y:
Horizontal = y
Diagonal = y + 1
Total = y + (y + 1) = 2y + 1
Conclusion: The expressions are correct and they do indeed add up to 2y + 1.

Page 102

Figure it out

For the problems asking you to find suitable expression(s), first try to understand the relationship between the different quantities in the situation described. If required, assume some values for the unknowns and try to find the relationship.

1. One plate of Jowar roti costs ₹30 and one plate of Pulao costs ₹20. If x plates of Jowar roti and y plates of pulao were ordered in a day, which expression(s) describe the total amount in rupees earned that day?
(a) 30x + 20y
(b) (30 + 20) × (x + y)
(c) 20x + 30y
(d) (30+20) × x + y
(e) 30x – 20y
Solution:
Jowar roti plate = ₹30
Pulao plate = ₹20
Jowar roti ordered in a day = x
Pulao plate ordered in a day = y
Total amount earned in a day = ₹(x × 30) + (y + 20) = 30x + 20y.
∴ (a) 30x + 20y is the required expression.

2. Pushpita sells two types of flowers on Independence day: champak and marigold. ‘p’ customers only bought champak, ‘q’ customers only bought marigold, and ‘r’ customers bought both. On the same day, she gave away a tiny national flag to every customer. How many flags did she give away that day?
(a) p + q + r
(b) p + q + 2r
(c) 2 × (p + q + r)
(d) p + q + r + 2
(e) p + q + r + 1
(f) 2 × (p + q)
Solution:
Customers bought champak = p
Customers bought marigold = q
Customers bought both = r
A national flag was given to every customer.
Total national flags distributed = p + q + r.
∴ (a) p + q + r is the required expression.

3. A snail is trying to climb along the wall of a deep well. During the day it climbs up ‘u’ cm and during the night it slowly slips down ‘d’ cm. This happens for 10 days and 10 nights.
(a) Write an expression describing how far away the snail is from its starting position.
(b) What can we say about the snail’s movement if d > u?
Solution:
(a) Snail’s movement in a day and night = (u – v) cm
Snail’s movement in 10 days and 10 nights = 10(u – v) cm
Total distance moved by the snail from its starting position = 10(u – v) cm

(b) if d > u, then the snail would slip more during night than it climbs each day and can never reach the height of the well.

4. Radha is preparing for a cycling race and practices daily. The first week she cycles 5 km every day. Every week she increases the daily distance cycled by ‘z’ km. How many kilometers would Radha have cycled after 3 weeks?
Solution:
Distance cycled in first week = 7 × 5 = 35 km
Distance cycled in second week = 7 × (5 + z) = (35 + 7z) km
Distance cycled in third week = 7 × (5 + z + z) = 7(5 + 2z) = (35 + 14z) km
Total distance cycled after 3 weeks = 35 + (35 + 7z) + (35 + 14z) = 35 + 35 + 7z + 35 + 14z
= (105 + 21z) km.

5. In the following figure, observe how the expression w + 2 becomes 4w + 20 along one path. Fill in the missing blanks on the remaining paths. The ovals contain expressions and the boxes contain operations.

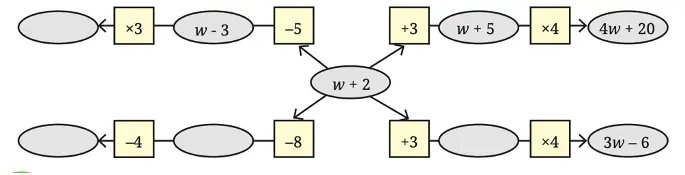
Solution:
Top left: (w + 2) → (-5) → (w – 3) → (×3) → 3w – 9.

Bottom left: (w + 2) → (-8) → (w – 6) → (-4) → (w – 10).

Bottom right: (w + 2) → (+3) → (w + 5) → (×4) → (4w + 20).

6. A local train from Yahapur to Vahapur stops at three stations at equal distances along the way. The time taken in minutes to travel from one station to the next station is the same and is denoted by t. The train stops for 2 minutes at each of the three stations.
(a) If t = 4, what is the time taken to travel from Yahapur to Vahapur?
(b) What is the algebraic expression for the time taken to travel from Yahapur to Vahapur? [Hint: Draw a rough diagram to visualise the situation]
Solution:

There are 4 segments of travel.
Trains stops 2 minutes at each station (S1, S2, S3).
Time taken to travel from one station to the next station = t
(a) If t = 4,
Total time taken to travel from Yahapur to Vahapur = 4 × 4 + 3 × 2 = 16 + 6 = 22 minutes.

(b) Time taken to travel from one station to another = t.
There are 4 segments and 3 stops of 2 minutes.
Algebraic expression = 4 × t + 3 × 2 = (4t + 6) minutes.

7. Simplify the following expressions:
(a) 3a + 9b – 6 + 8a – 4b – 7a + 16
(b) 3(3a – 3b) – 8a – 4b – 16
(c) 2(2x – 3) + 8x + 12
(d) 8x – (2x – 3) + 12
(e) 8h – (5 + 7h) + 9
(f) 23 + 4(6m – 3n) – 8n – 3m – 18
Solution:
(a) 3a + 9b – 6 + 8a – 4b – 7a + 16
= 3a + 8a – 7a + 9b – 4b – 6 + 16
= 11a – 7a + 5b + 10
= 4a + 5b + 10.

(b) 3(3a – 3b) – 8a – 4b – 16
= 9a – 9b – 8a – 4b – 16
= 9a – 8a – 9b – 4b – 16
= a – 13b – 16.

(c) 2(2x – 3) + 8x + 12
= 4x – 6 + 8x + 12
= 4x + 8x – 6 + 12
= 12x + 6.

(d) 8x – (2x – 3) + 12
= 8x – 2x + 3 + 12
= 6x + 15.

(e) 8h – (5 + 7h) + 9
= 8h – 5 + 7h + 9
= 8h + 7h + 9 – 5
= 15h + 4.

(f) 23 + 4(6m – 3n) – 8n – 3m – 18
= 23 + 24m – 12n – 8n – 3m – 18
= 24m – 3m – 12n – 8n + 23 – 18
= 21m – 20n + 5.

8. Add the expressions given below:
(a) 4d – 7c + 9 and 8c – 11 + 9d
(b) –6f + 19 – 8s and –23 + 13f + 12s
(c) 8d – 14c + 9 and 16c – (11 + 9d)
(d) 6f – 20 + 8s and 23 – 13f – 12s
(e) 13m – 12n and 12n – 13m
(f) –26m + 24n and 26m – 24n
Solution:
(a) 4d – 7c + 9 and 8c – 11 + 9d
= 4d – 7c + 9 + 8c – 11 + 9d
= 4d + 9d – 7c + 8c + 9 – 11
= 13d + c – 2.

(b) –6f + 19 – 8s and –23 + 13f + 12s
= –6f + 19 – 8s + (–23) + 13f + 12s
= -6f + 13f – 8s + 12s + 19 – 23
= 7f + 4s – 4.

(c) 8d – 14c + 9 and 16c – (11 + 9d)
= 8d – 14c + 9 + 16c – (11 + 9d)
= 8d – 14c + 9 + 16c – 11 – 9d
= 16c – 14c + 8d – 9d + 9 – 11
= 2c – d – 2.

(d) 6f – 20 + 8s and 23 – 13f – 12s
= 6f – 20 + 8s + 23 – 13f – 12s
= 6f – 13f + 8s – 12s – 20 + 23
= -7f – 4s + 3.

(e) 13m – 12n and 12n – 13m
= 13m – 12n + 12n – 13m
= 13m – 13m – 12n + 12n
= 0.

(f) –26m + 24n and 26m – 24n
= -26m + 24n + 26m – 24n
= -26m + 26m + 24n – 24n
= 0.

9. Subtract the expressions given below:
(a) 9a – 6b + 14 from 6a + 9b – 18
(b) –15x + 13 – 9y from 7y – 10 + 3x
(c) 17g + 9 – 7h from 11 – 10g + 3h
(d) 9a – 6b + 14 from 6a – (9b + 18)
(e) 10x + 2 + 10y from –3y + 8 – 3x
(f) 8g + 4h – 10 from 7h – 8g + 20
Solution:
(a) 9a – 6b + 14 from 6a + 9b – 18
= 6a + 9b – 18 – (9a – 6b + 14)
= 6a + 9b – 18 – 9a + 6b – 14
= 6a – 9a + 9b + 6b – 18 – 14
= 3a + 15b – 32.

(b) –15x + 13 – 9y from 7y – 10 + 3x
= 7y – 10 + 3x – (–15x + 13 – 9y)
= 7y – 10 + 3x + 15x – 13 + 9y
= 7y + 9y + 3x + 15x – 10 – 13
= 16y + 18x – 23.

(c) 17g + 9 – 7h from 11 – 10g + 3h
= 11 – 10g + 3h – (17g + 9 – 7h)
= 11 – 10g + 3h – 17g – 9 + 7h
= -10g -17g + 3h + 7h + 11 – 9
= -27g + 10h + 2.

(d) 9a – 6b + 14 from 6a – (9b + 18)
= 6a – (9b + 18) – (9a – 6b + 14)
= 6a – 9b – 18 – 9a + 6b – 14
= 6a – 9a – 9b + 6b – 18 – 14
= -3a – 3b – 32.

(e) 10x + 2 + 10y from –3y + 8 – 3x
= -3y + 8 – 3x – (10x + 2 + 10y)
= -3y + 8 – 3x – 10x – 2 – 10y
= -3x – 10x – 3y – 10y + 8 – 2
= -13x – 13y + 6.

(f) 8g + 4h – 10 from 7h – 8g + 20
= 7h – 8g + 20 – (8g + 4h – 10)
= 7h – 8g + 20 – 8g – 4h + 10
= -8g – 8g + 7h – 4h + 20 + 10
= -16g + 3h + 30.

10. Describe situations corresponding to the following algebraic expressions:
(a) 8x + 3y
(b) 15x – 2x
Solution:
(a) 8x + 3y
Ramesh buys 8 pencils, each costing ₹x, and 3 pens, each costing ₹y.
Total cost = 8x + 3y

(b) 15x – 2x
A shopkeeper has 15 boxes, each containing x apples. He sells 2 boxes.
Apples left = 15x − 2x = 13x.

11. Imagine a straight rope. If it is cut once as shown in the picture, we get 2 pieces. If the rope is folded once and then cut as shown, we get 3 pieces. Observe the pattern and find the number of pieces if the rope is folded 10 times and cut. What is the expression for the number of pieces when the rope is folded r times and cut?

Solution:
No fold: 1 cut → 2 pieces.
1-fold: 1 cut → 3 pieces.
2-fold: 1 cut → 4 pieces.
3-fold: 1 cut → 5 pieces.
Similarly,
For 10-fold: 1 cut → 11 pieces.
Expression with ‘r’ times fold and cut = r + 2.

12. Look at the matchstick pattern below. Observe and identify the pattern. How many matchsticks are required to make 10 such squares. How many are required to make w squares?

Solution:
1 square → 4 matchsticks.
2 squares → 7 matchsticks.
3 squares → 10 matchsticks.
Similarly,
For 10 squares → 31 matchsticks.
Matchsticks required to make ‘w’ squares = 3 × w + 1 = 3w + 1.

13. Have you noticed how the colours change in a traffic signal? The sequence of colour changes is shown below. Find the colour at positions 90, 190, and 343. Write expressions to describe the positions for each colour.

Solution:
Red positions: 1, 5, 9, 13…….
Yellow positions: 2, 4, 6, 8, 10…….
Green positions: 3, 7, 11, 15…….

Expression for red colour = 4r – 3.
Expression for yellow colour = 2y.
Expression for green colour = 4g – 1.

Red: Numbers that are 1 more than multiples of 4 (Remainder 1 when divided by 4)
Yellow: All even numbers (Remainder 0 when divided by 4)
Green: Numbers that are 3 more than multiples of 4 (Remainder 3 when divided by 4)

90 and 190: Both are even → Yellow
343 ÷ 4 = 85 R3 → Remainder = 3 → Green

14. Observe the pattern below. How many squares will be there in Step 4, Step 10, Step 50? Write a general formula. How would the formula change if we want to count the number of vertices of all the squares?

Solution:
Step 1: 5 squares.
Step 2: 9 squares.
Step 3: 13 squares.
General formula: 4n + 1
Step 4: 4(4) + 1 = 16 + 1 = 17
Step 10: 4(10) + 1 = 40 + 1 = 41
Step 50: 4(50) + 1 = 200 + 1 = 201

For vertices;
Step 1 → 20
Step 2 → 36
Step 3 → 52
General formula: 16n + 4.